Лекция 6

Теория графов, познакомьтесь

Материалы	Ссылка
Видео	YouTube
Слайды	pdf
Конспект	скоро :)
Домашнее задание	здесь

Видео

Предисловие

Данная лекция носит ознакомительный характер и её цель - показать, где в математике начинается красота. Теория графов - увлекательная область знаний, почти три века остававшаяся уделом узкого круга специалистов, начинает привлекать внимание всё более широкой аудитории, количество приложений и задач прирастает (с текущим состоянием дел в области всегда можно сверится здесь [1] ). На мой взгляд, данный матаппарат - это вторая по элегантности идея из когда-либо представленных публике в Санкт-Петербурге и несомненно - одно из самых значимых открытий первой космической цивилизации, основанной викингами на склонах Днепра.

Для начала стоит определиться с тем, чем эта лекция не является. Это - не глубокий методический материал, покрывающий все детали рассматриваемых вопросов. Желающим ознакомиться с текущим состоянием дел в машинном обучении на графах стоит обратить внимание на курс cs224w [2], материалы которого отражают видение области (ограниченное форматом 20 лекций за 10 недель) от одной из самых продуктивных исследовательских группировок планеты. С классической теорией графов весьма здорово знакомит книга Фрэнка Харари [3], в момент написания данного текста вышел ещё один весьма подробный обзор [4] существующих техник анализа сетей, а лучшего рассказа о механике работы PageRank, чем лекция Юре Лесковца 2017 года [5] мне ещё не встречалось. Впрочем, в киевском политехе бытует мнение: кто умеет - делает; кто не умеет - учит; а кто даже учить неспособен - методологией занимается и учит как учить следует.

Данная часть курса предполагает существенную практическую нагрузку и это отражает мнение о том, что лучше всего запоминается сделанное лично. Домашнее задание поможет убедиться в том, как и почему работает движок поиска Google первой версии, а для желающих добавки предусмотрена возможность выполнить проект и решить задачу предсказания связи. Надеюсь, что решение задачек развлечёт вас и подстегнёт желание разобраться с предметом глубже и шире.

Я с удовольствием просмотрю решения, набирающие более 60 баллов из доступных 75 за условно обязательную часть задания (все 100 можно собрать, выполнив проект) и для выбравших способы реализации, кажущиеся мне оптимальными, откроются дополнительные возможности.

■ Знакомство

Вступление и контекст | 1-9

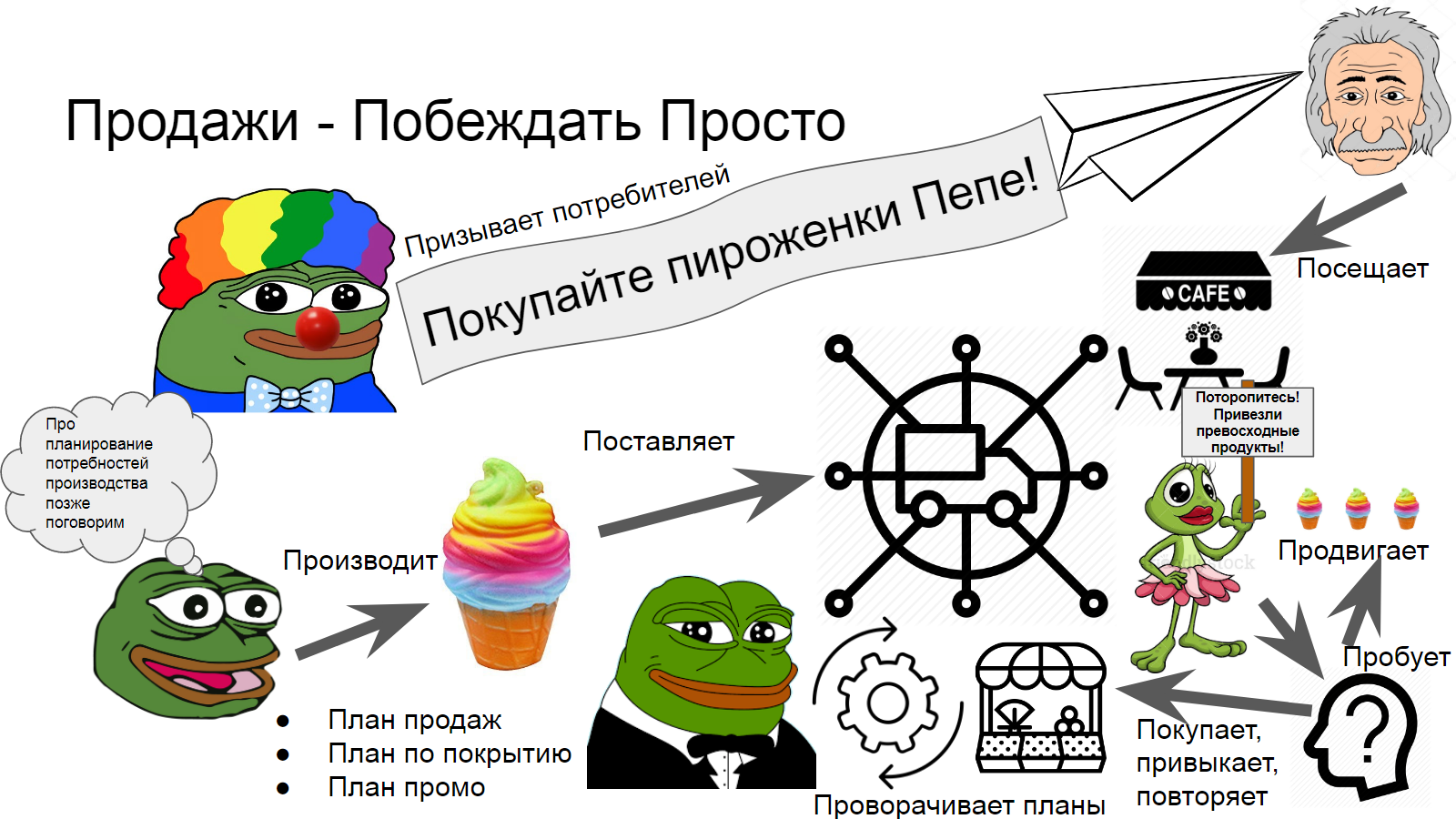
Анализ данных должно начинать с понимания бизнеса, поэтому для начала мы познакомимся с лягушонком-предпринимателем, его подчинёнными, любимыми клиентами, а также - первой незадачей, заставляющей задуматься о необходимой перемене состояния дел.

Итак, зададим контекст. Познакомьтесь с Пепе. Пепе - лягушонок-предприниматель. Он делает пироженки, которые любит Альберт.

На самом деле они и не встречались ни разу. Пепе производит пироженки и сбывает их через розницу, а Альберт - ходит в любимое кафе. Кроме того, есть ещё много разных торговых точек, которые различаются форматом, ассортиментом, и в целом - тем опытом, который получает в них потребитель.

Соответственно, классификация мест продажи товаров по опыту потребителей называется управлением каналами продаж. И входит в дисциплину управления взаимоотношениями с клиентами, которой я занимаюсь с 2004 года. Управление отношениями с клиентами (Customer Relationship Management, CRM, или как его недавно начали называть Customer Experience (Management), CX(M)) - это системный подход ориентации бизнеса на потребности клиента с целью создания максимально успешного персонализированного подхода.

Очевидно, что наш лягушонок стремится захватить рынок и продвигать пироженки в максимальном количестве точек.

По мере роста бизнеса и выхода на национальный уровень продаж, количество посредников на пути пироженки от Пепе к Альберту увеличивается. Появляются региональные дистрибьюторы с их складами, оптовики и вся эта сеть дистрибуции. Задачей команды продаж является обеспечить покрытие розницы необходимым ассортиментом продукции и обеспечение её достаточным уровнем запасов для того, чтобы максимально свежие пироженки были доступны всем желающим.

Ребята из маркетинга проводят кампании по привлечению потребителей к бренду, стремясь в идеале к тому, чтобы любители сладкого становились настолько лояльными, что не только бы приходили за пироженками, но и в ситуации, когда их не нашлось - шли в соседний магазин и требовали продукции привычной торговой марки.

Кроме воспитания лояльности, есть ёще задача расширения аудитории. Для этого в рознице проводят промо, размещают промоутеров, рекламную продукцию, и дегустации устраивают (для этого команде продаж приходится ещё и доставкой образцов озадачиваться).

В продажах есть три вида планов:

Собственно, сам план продаж - нам нужно обеспечить объемы, например продавать вагон пироженок каждую неделю;
План по покрытию торговых точек - мы говорим дистрибуции (нумерической, когда считаем количество точек, в которых присутствует продукция, и взвешенной, которая определяется как доля полки - торгового пространства занятого категорией продукции, включая конкурентов);
План промо - всякий раз, когда мы что-то покупаем со скидкой, этот праздник жизни оплачен производителем, которому нужно заранее договориться со всеми точками о сроках и условиях проведения акции).

О том, как действия команд продаж и маркетинга влияют на производственные планы - отдельный разговор. Мы ведь всё это делаем для стимуляции спроса, верно? Согласовать и синхронизировать всю эту деятельность - плёвое дело. Выигрывать легко и чемпионом мира может стать каждый.

Коллеги из маркетинга любят цитировать Дэвида Огилви и повторять мантру “Мы знаем, что работает только половина из того, что мы делаем, но не знаем какая!” И очень расстраиваются, когда я им в ответ сообщаю, что половина работала у Дэвида потому что он был гений рекламы, а у простых смертных - лишь треть промо выходит в безубыточность и называть это “работает” - слишком смело.

В 2014 компания Nielsen провела глобальное исследование ситуации [6] и выводы - неутешительны. Всё больше средств тратится на продвижение в рознице со всё уменьшающейся эффективностью. Вообще, если посмотреть на историю вопроса, а первые упоминания о практике трейд-маркетинга датируются концом 70-х годов прошлого века, то мы видим стабильный рост данной статьи затрат в отчётах о прибылях и убытков и с 5% в 1978 затраты в среднем по индустрии потребительских продуктов достигли четверти товарооборота в 2015. На тот момент в деньгах весь этот совокупный бюджет был равен триллиону долларов США - или номиналу всех имевшихся на планете стодолларовых купюр.

Управление изменениями организации | 10-14

Перемен требуют наши сердца, да вот только мир вокруг - весьма консервативен. Посмотрим, как коллективы реагируют на новаторство и задумаемся, каким образом ситуацию описать.

Собрал Пепе своих деятелей продаж и маркетинга и стали они разбор полётов проводить. До истины докапываться, пытаясь понять, как же вышло так, что акцию запустили, ценники напечатали, промоутеров поставили, а скидку в систему не ввели. Оказывается, у ребят из маркетинга все планы в аккуратных табличках, а у отдела продаж - даже база данных есть.

И специалистов много (на деле в компании - игроке национального уровня это будет несколько сотен человек), и табличек хватает.

В общем посмотрел на это наш лягушонок, вспомнил лекции об управлении информационными системами, да и предложил все данные в одной интегрированной системе хранить. Воспользоваться, так сказать, лучшими практиками. И тут что маркетинг, что продажи - прямо засветились от счастья.

Сила - привычки - страшная сила. И эта волна счастья и любви - сразу же распространяется по организации, так что на нашего лягушонка-инноватора начинают коситься в коридорах даже подчинённые подчинённых подчинённых.

Сел Пепе, обнял коленки лапками, загрустил. Вспомнил, что ещё в середине прошлого века Эверетт Роджерс придумал теорию диффузии инноваций [7], согласно которой лишь небольшая доля граждан позитивно воспринимает всё новое - примерно 2.5% от популяции, следующая группа ценителей нового - ранние пользователи - более придирчива и делает рациональный выбор, таких около 13.5%, за ними следит раннее большинство, руководствующееся логикой и следующее за лидерами мнений из числа ранних пользователей - следующие 34% (в сумме - уже половина). За ними следует позднее большинство, и тормоза, которые склоняются к новому когда деваться уже некуда. Также лягушонок впомнил о том, что все эти инновации распространяются в социальной структуре, которая несколько богаче формальных отношений подчинённсти. Вспомнил, да и попробовал всё описать.

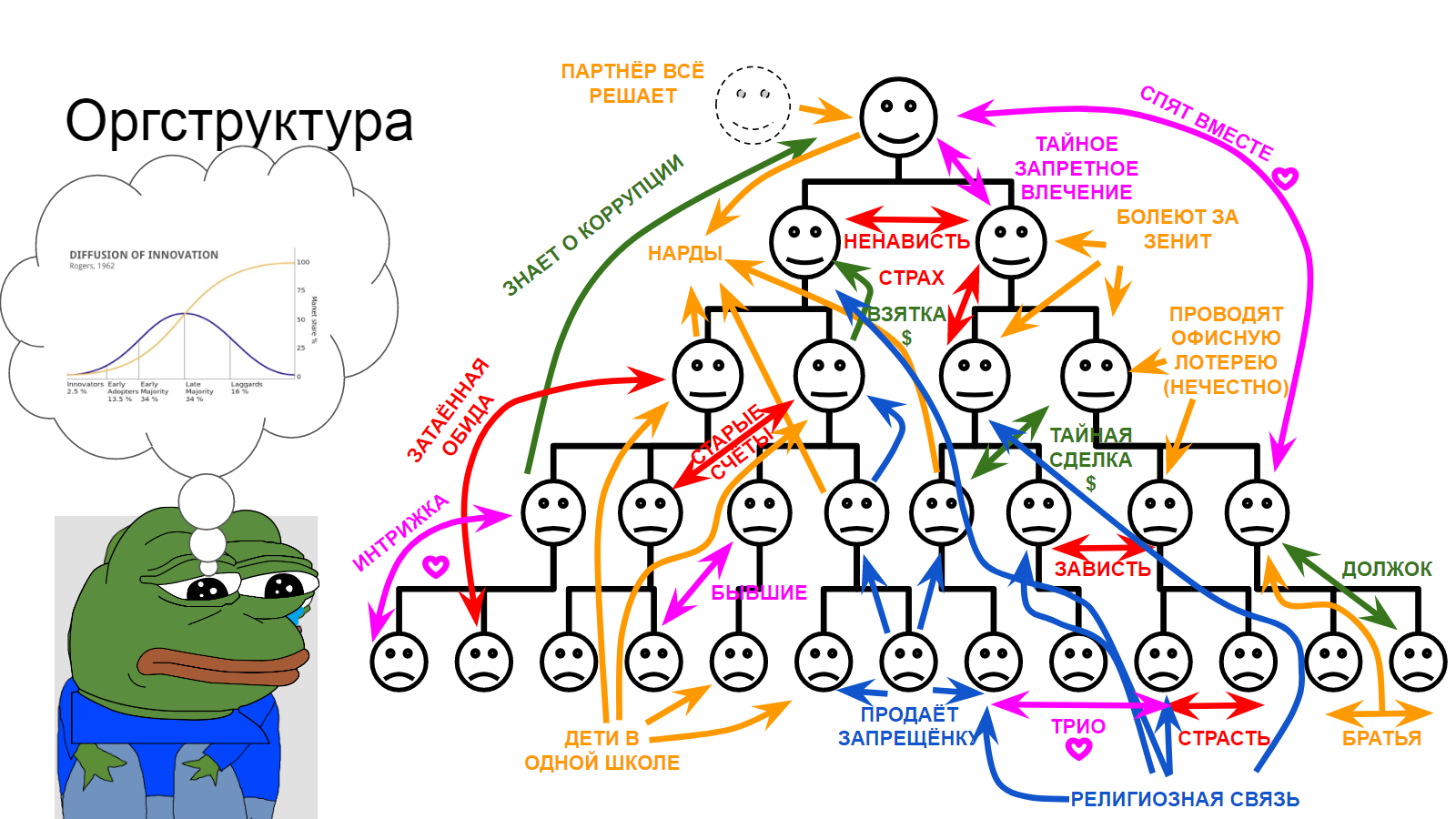
А описывать было чего. Тут и дружба по общему делу. И сильные чувства. Финансовые связи. Общность духовных поисков. Не говоря уже о делах любовных.

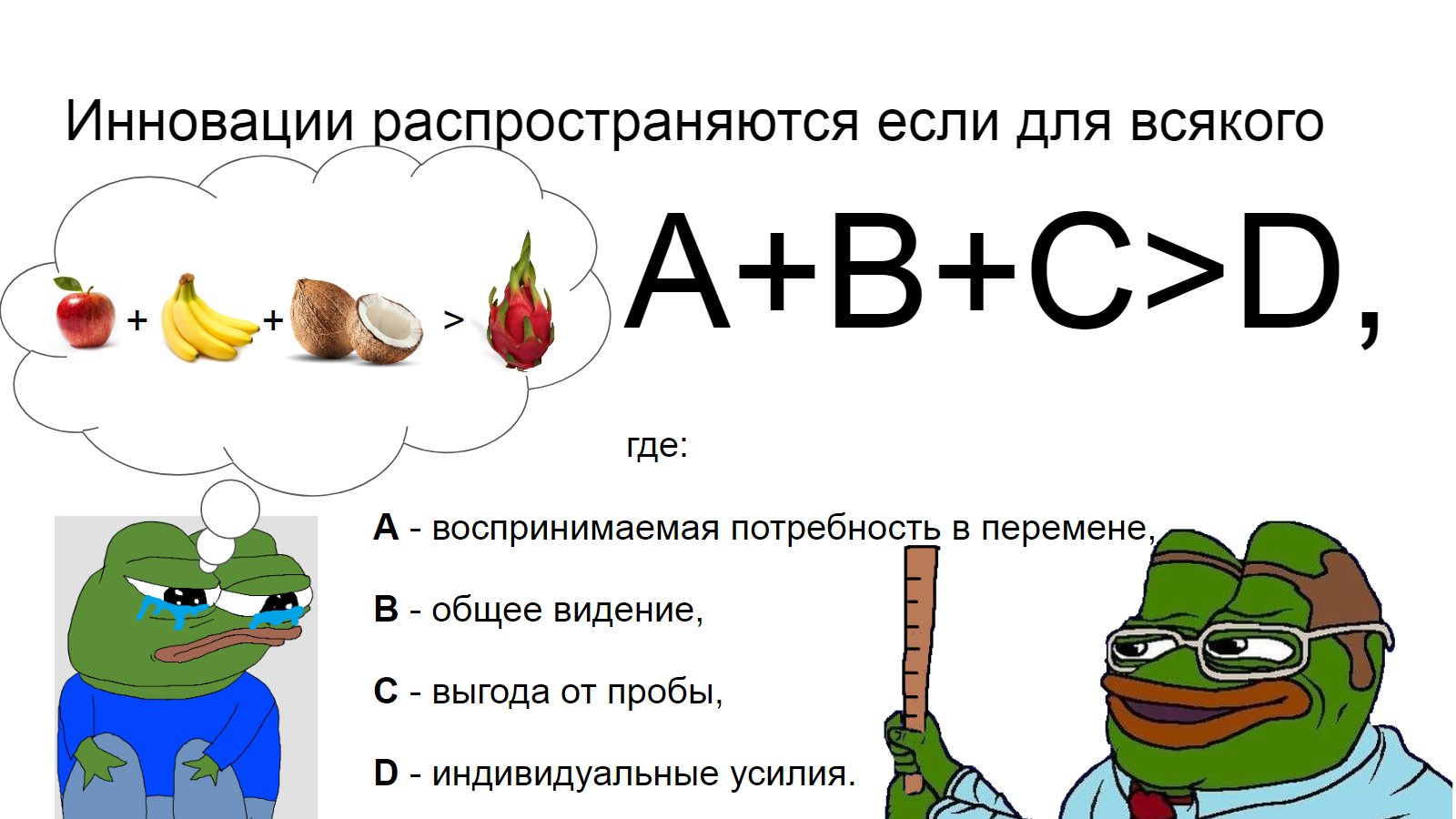
Организационные изменения - это просто. Достаточно убедиться в том, что для всякого, кого перемены задевают (стейкхолдерами - так в дисциплине управления проектами называют лица и организации, имеющие влияние на проект, либо же наоборот тех, на кого инициатива повлияет), верно следующее неравенство:

\[ A + B + C > D \]

В нём: \[ А \] (воспринимаемая потребность в переменах), например - не работают промо и это недопустимо, ситуацию необходимо менять, вместе с \[ В \] (общим видением), например - мы все понимаем, что хранение данных в разрозненных системах - непрозрачно и приводит к сбоям в рабочих процессах, и \[ С \] (немедленная выгода от нового) - быстрая победа, вроде повышения ключевых показателей, вроде возврата инвестиций в продвижение продукции в рознице, вместе взятые, перевесят \[ D \] - необходимые для воплощения перемен усилия.

Если неравенство выполняется для каждого стейкхолдера по отдельности, то перемены будут происходить легко.

Остаётся лишь разобраться с тем, какая алгебра позволяет подобные выкладки.

Попытки всё эту уйму связей осмыслить и упорядочить - вызывают сильную головную боль и вообще расстройство. Как это часто бывает, выбор - невелик.

Либо красная таблетка - матричные методы и это вот всё.

Либо синяя - и шанс на какое-то время снова стать беззаботным лягушонком. Ненадолго.

Но наш лягушонок - не так-то прост. Хочется ведь всего и сразу. Хватает он обе таблетки…

И Альберт остаётся без пироженок.

Общий язык и формальная запись | 15-18 *

Теория графов даёт нам способ описания связных систем. Ознакомимся со способом записи и основными понятиями.

Здесь и далее звёздочкой (*) отмечены разделы, непосредственно относящиеся к домашнему заданию.

Что мы можем вынести из этих трёх примеров?

Первое и самое очевидное - связи важны. Будь то менеджмент или маркетинг. Или фармакология. Собственно, острие прогресса современной математики проходит в области биоинформатики и самый простой способ быть впереди конкурентов - это следить за исследованиями вроде этого - и переносить их в контекст маркетинга, например.

Поясню детальнее. В данной работе [8] Маринка Житник предложила оценивать побочные эффекты от совместного приёма препаратов, не возникающие по отдельности. В США 39% людей старше 65 принимают пять или более препаратов одновременно и тестировать все возможные комбинации на совместимость долго, дорого, да и на людях не разрешат.

Похоже на маркетинговые тактики, верно? Один директор по развитию одной большой компании - лидера рынка, продукцию которой большинство из вас наверняка пробовали, как-то раз в частной беседе сказал: “Мы не знаем, что работает, поэтому делаем всё. Зачастую - просто не даём шанс купить нашу продукцию без скидки”.

Сети - общий язык описания сложных систем, позволяющий наработки из одной области легко переносить в другую.

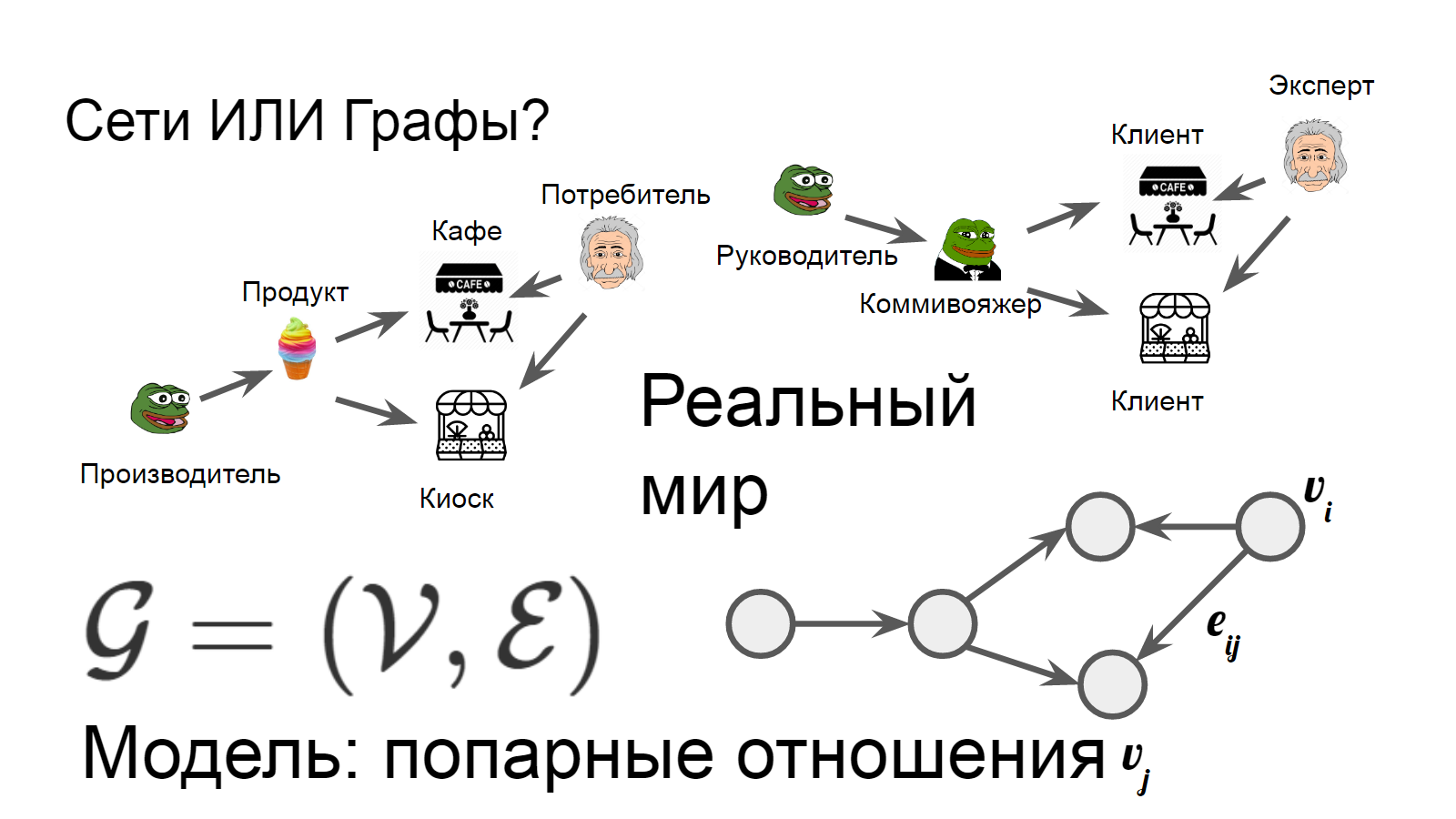
Сети или графы?

В реальном мире мы наблюдаем астрономические тела и их взаимодействия.

В мире фантазий - оперируем моделями - множествами множеств.

Добавим формальностей. Теория графов оперирует множествами сущностей и их связей. Сущности называют вершинами или узлами, иногда даже делают кальку с английского и зовут их нодами. Взаимодействия сущностей называют рёбрами (иногда - арками) и связями. Систему же сущностей и их отношений называют графом или сетью. При этом сеть обычно относится к объектам реального мира, а граф - это математическая модель. Соответственно, вершины и рёбра - формальные математические названия, а узлы и связи - скорее прикладные термины. Мы их будем рассматривать как эквивалентные.

В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V × V, то есть его декартова произведения на самого себя - всех возможных попарных комбинаций из двух вершин.

■ Наблюдения

Типы связей | 19-21

Связи - всякие случаются, рассмотрим несколько примеров построения графов для различного рода взаимодействий и познакомимся с понятием проекций.

Связи бывают разного характера. Простейший случай - неориентированные рёбра. Они описывают попарные отношения, в которых обе сущности - равнозначны. Например - соавторство или дружба в соцсети. Несколько учёных написали статью и вот вам связь соавторства - работали над чем-то вместе. С соцсетями пример заковыристей - если мы рассматриваем просто отношение дружбы, то непросто выделить кто из двоих сильнее дружит. Всё же сейчас есть функционал подписок, когда незнакомые люди могут отслеживать чьи-то открытые публикации. И это неравновесное отношение выражается ориентированным ребром.

Так, например, организован Твиттер. Или телефонные звонки - есть вызывающая сторона, а есть - вызываемая. Отправитель и получатель сообщения. То есть простейшим способом рассуждать о графах будет разделение их на ориентированные и неориентированные.

Связи разные бывают. Например, между одни и те же люди могут быть соавторами, друзьями в соцсети, переписываться, созваниваться голосом и по видеосвязи, ходить на вечеринки и посещать спортивную секцию.

В альма-матер, когда учился на связита, приучили разделять передачу сообщений по родам (в зависимости от физических принципов передачи - проводная, радио, оптическая, и т.д.) и видам (тип передаваемой информации - видео, текст, аудио и т.д.) связи. Так что, когда будете изображать связи разного вида и рода, мой вам совет - запасайтесь цветными карандашами.

Формально, в теории графов рассуждают о модах - принципиальных способах взаимодействия между сущностями и графы с несколькими типами взаимодействий называют мультимодальными. Кроме того, сущности тоже бывают разными.

Например, обед в столовке можно описать графом, в котором посетитель, заведение, блюдо, повар, и поварёнок на раздаче будут разными сущностями, которых связывает отдельный акт гастрономии. Формально такие графы называются многодольными. В них доли общего множества вершин соответствуют классификации объектов. В общем случае мы рассуждаем о гетерогенном графе, в котором разнообразные сущности взаимодействуют различным образом.

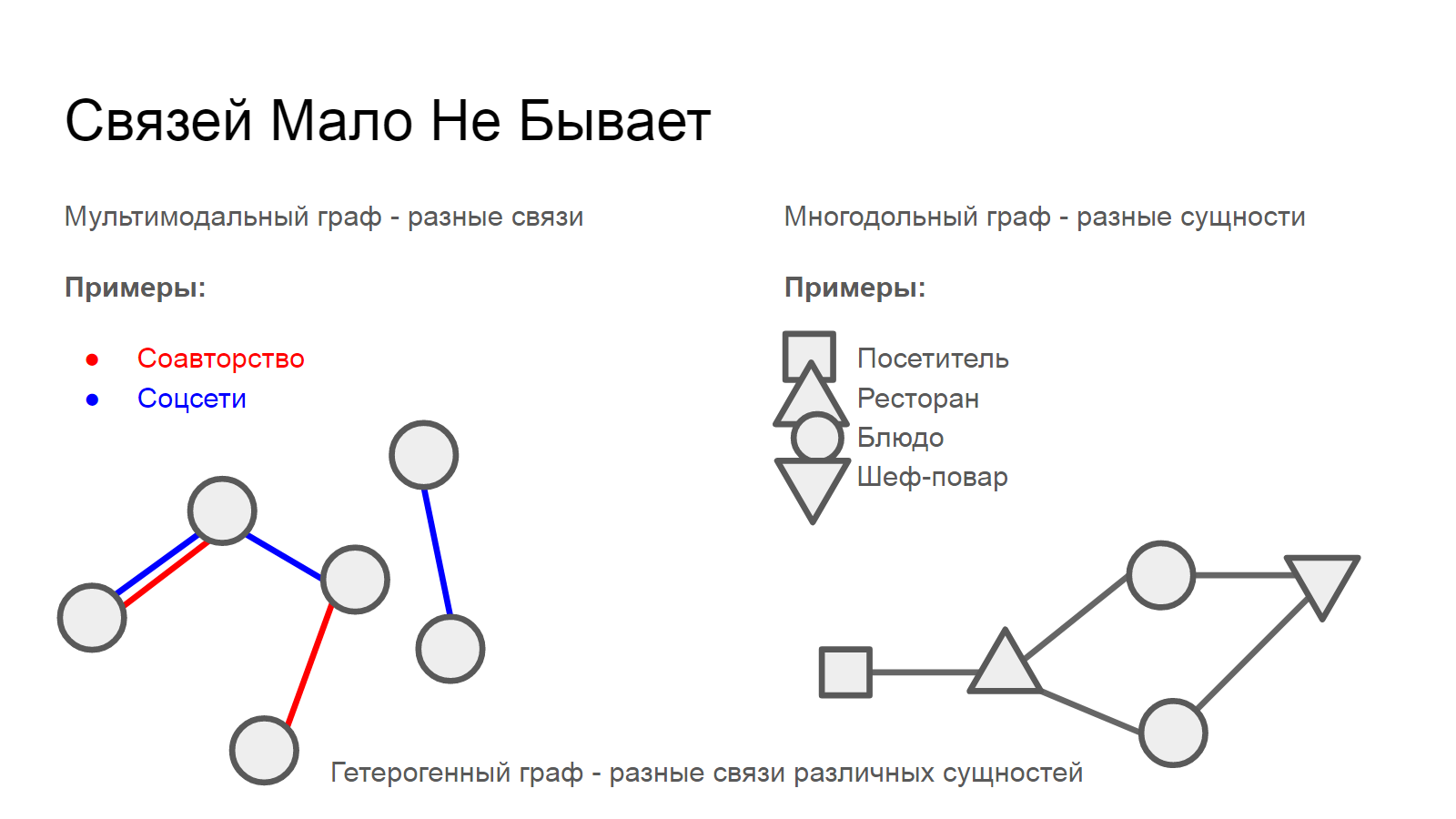
Об одной и той же ситуации можно размышлять по-разному. И графы строить разнообразные. Так, двудольный граф, описывающий посещения нескольких ресторанов разрозненной группой товарищей эквивалентно проецируется в два однодольных графа: товарищей, пересекающихся в одном заведении и заведений с пересекающейся аудиторией. В общем, из одной и той же ситуации и набора данных можно наделать очень много графа, главное - понимать что вы делаете и помнить о том, что полносвязные области могут дорого обойтись в плане вычислительной нагрузки. Но о связности - чуть позже.

Рост, пути, уплотнение | 22-24 *

Здесь мы рассмотрим последовательный процесс формирования графа из поступающих данных и обозначим такие понятия, как: вес рёбер, дистанция между вершинами и диаметр графа.

Сначала посмотрим на то, как граф растёт.

Обычно мы строим модель из каких-то данных, например потоков транзакций или регистрации сайтов в сети. Сначала появляются вершины (но может быть и случай, когда регистрируется телефонный звонок и тогда у нас сразу есть первое ребро, соединяющее две вершины). Затем между ними возникают рёбра. По мере роста количества рёбер на графе образуются пути. Путь - это последовательность соединённых между собой вершин. Его можно записать как множество вершин,

\[ P_n = \{ i_0, i_1, i_2, … , i_n \} \]

либо же множество рёбер.

\[ P_n = \{(i_0, i_1),(i_1, i_2),(i_2, i_3), … ,(i_{n-1}, i_n )\} \]

Путь может пересекать сам себя - как траектория движения в физике.

Дистанцией на графе (геодезической) называется длина кратчайшего пути меж двух вершин. Для пары несвязных вершин дистанция равна бесконечности.

По мере наблюдения за происходящим мы замечаем, что некоторые события, то есть взаимодействия между сущностями повторяются.

И это нам позволяет различать вес рёбер. Простейшим случаем будет просто просуммировать все инциденты на наблюдаемом временном интервале. А в общем случае - мы можем определить вес ребра как функцию от некоего множества параметров.

Например - представьте себе некий режимный объект вокруг которого установлено несколько линий заграждения, опутанных сеткой проводов. Группа товарищей - пытается перебраться через эту полосу препятствий. Каждый удар электрического разряда в забор будет его разогревать на несколько градусов. А потом раскалённый металл будет остывать. Ваша задача - определить необходимую частоту ударов и найти элементы конструкции, которым стоит больше всего внимания уделить. Так, чтобы и объект остался режимным, и электричество расходовать экономно и беречь таким образом планету. В общем, рассматривать граф статичным объектом - скучно.

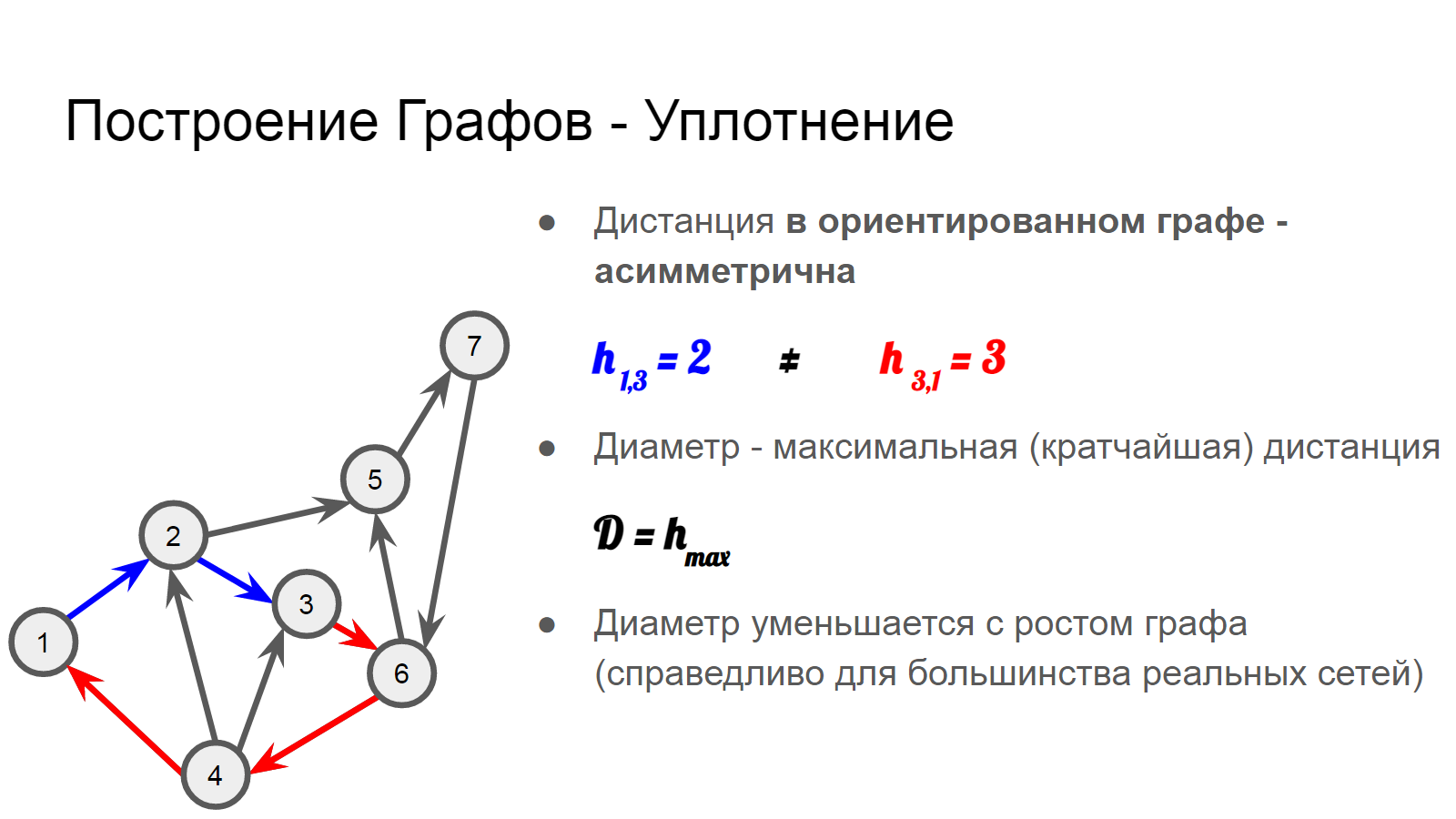
Обратите внимание на то, что путь в ориентированном графе предполагает движение по направлению рёбер. То есть дистанция - асиметрична. Например, из вершины 1 в вершину 3 мы доберёмся за два шага, а обратного пути нет.

Диаметр графа - одна из первых статистик, позволяющих измерять сети - длина наибольшего кратчайшего пути, отличного от бесконечности. По мере роста графа, образовываются новые рёбра и в большинстве реальных систем мы наблюдаем уменьшение диаметра. Так называемое сжатие.

Связность и компоненты | 25-26 *

Неравномерность характера связей в окружающей нас природе - скорее правило, исключение из которого - кристаллы, приводит нас определению связности как свойства графа. Характер соединённости определяет свойства системы - например, в телекоме хорошо бы иметь возможность установить соединение между географически разнесёнными узлами и для этого необходимым условием будет связность графа сети связи.

Важное свойство графов - связность. То есть проходимость между вершинами по рёбрам. Именно связность графа интернет подтолкнула развитие методов случайных блужданий, о которых подробно поговорим чуть позже.

Вообще, интернет можно описать несколькими способами. Например, это могут быть физические линии связи - магистральные кабели, проложенные между континентами. Также можно рассуждать о маршрутизации пакетов на транспортном уровне - и моделировать сетевое оборудование.

Мы же рассмотрим структуру всемирной паутины гипертекста - сайты и гиперссылки между ними. Для каждой страницы, связанной с прочими посредством гиперссылок, нас интересуют два вопроса: (1) куда можно забраться, переходя по ссылкам и (2) откуда можно попасть по ссылкам в эту самую страницу - в обоих случаях нас интересует множество страниц и его мощность.

Первое такое множество называют OutComponent, а второе - InComponent.

К примеру, для вершины #2 входящие рёбра приходят из 1 и 4, а исходящие - ведут в 3,5,6 и 7.

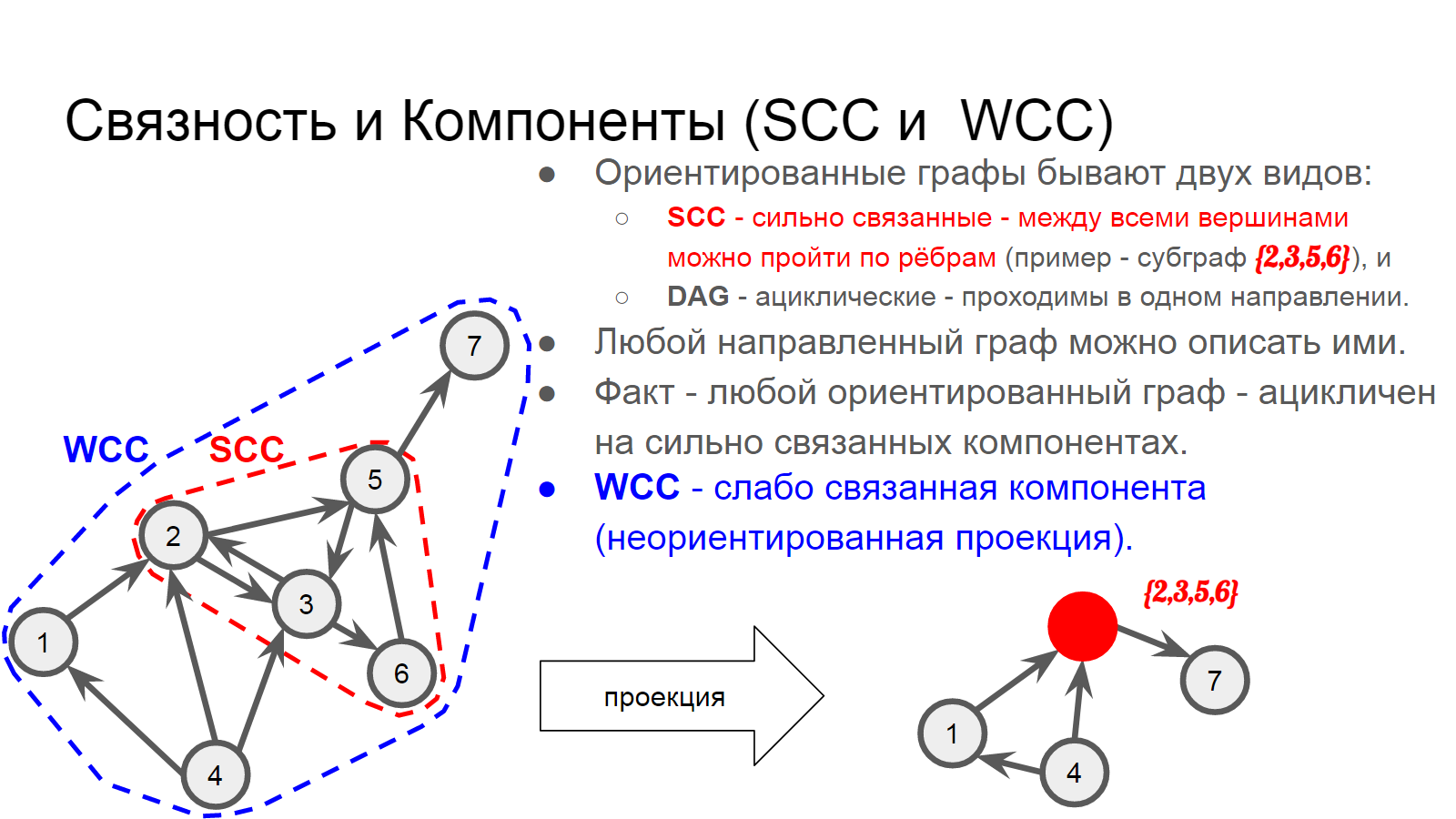
По мере роста графа, в нём образуются связанные компоненты из множества соединённых вершин. Ориентированные графы бывают двух видов: (1) сильно связанные - такие, что из любой вершины можно перейти в любую и (2) ациклические - в них проход по рёбрам возможен только в одном направлении.

Любой направленный граф можно представить как ациклическую композицию из сильно связанных компонент.

Такой способ “ужимания” графов - достаточно распространённая практика, позволяющая работать с проекциями и делать на основании их выводы, обобщающиеся на вершины, входящие в сильно связанные компоненты. Вообще, с дальнейшим ростом количества рёбер, граф может стремиться к полной связности.

Кроме сильной связности, рассматривают ещё и слабую связность - в этом случае мы обращаемся к неориентированной проекции и считаем две вершины связанными независимо от направления ребра между ними.

Форма интернет | 27-28 *

Была интригой вплоть до 1999 года!

Размышления о связности приводят нас к вопросу о форме интернета. Как-то раз я задал этот вопрос: “Как ты считаешь, какой формы интернет?” однокурснику, он задумался и выдал: “Ну он либо круглый, либо плоский!” На деле всё интереснее.

Проведём вычислительный эксперимент: (1) наугад выберем одну вершину i, (2) найдём её компоненты In(i) и Out(i), (3) вычислим их размеры.

Пересечением этих двух множеств и будет сильно связанная компонента SCC(i), в которой находится наша вершина.

Как это реализовать? Поиском вширь! [9] Для Out(i) всё очевидно - берём вершину, запускаем BFS и смотрим на получившееся в результате дерево. А как найти In(i)? Здесь мы вспомним, что из одного графа можно наделать множество проекций (ограничивающееся только фантазией и доступной памятью) и перевернём наш граф интернета.

Строго говоря, создадим G’ - проекцию G, в которой рёбра перевёрнуты в направлении противоположном оригинальному. И снова запустим BFS.

Повторим эксперимент в масштабе интернет. Первыми, кто задался этим вопросом были товарищи Andrei Broder, Ravi Kumar и Andrew Tomkins [10] - в конце прошлого тысячелетия у них были результаты прохода краулера Altavista - в октябре 1999 открытый публике интернет представлял собой 203M URL, между которыми было проложено 1.5B гиперссылок. Сделаем выборку из всего множества страниц и запустим BFS в обе стороны для каждой из них. Первое наблюдение: BFS либо обходит много страниц, либо затухает.

Посчитаем размеры In(i), Out(i) и SCC(i) для каждой вершины.

Оказывается, у веб - структура не круглая, и не плоская! Есть одна большая сильно связанная компонента - на заре интернета её размер был примерно четверть всех страниц (28%), также есть часть страниц, на которые можно перейти по ссылкам из SCC, это - наша Out-компонента (22%), и часть, из которой можно перейти в SCC (а затем - в OUT) - это наша In-компонента (22%). Часть ссылок ведёт из IN на сайты, не входящие в обозначенные компоненты, а также часть ссылок из сайтов, не входящих в компоненты, ведёт в OUT - такие ссылки называются щупальцами (Tendrils) - их в конце прошлого века было около 22%. Есть ещё ссылки из IN прямо в OUT - их называют трубами (Tubes). Вся эта структура вместе взятая - напоминает галстук-бабочку.

Есть ещё небольшое количество несвязанных с основной частью интернета островков-компонент.

Со временем веб подрос, пропорции компонент изменились (теперь SCC - доминирует, в 2014 она включала в себя уже больше половины всех страниц - [11]), но сама форма остаётся неизменной и за это исследование в 2017 даже вручили награду “Проверено временем” [12]. Подобная структура наблюдается во многих сетях - экономические транзакции, переписка, выставление оценок в соцсетях и так далее.

Триады, мотивы, центральность | 29-32

Кроме вершин и рёбер в графах рассматривают структуры среднего порядка размерности. Простейший случай - триады. Повторяющиеся структуры зовут мотивами и их характер зачастую определяет свойства системы и её частей. Также вскользь упомянём о том, как определяется центральность вершин и приведём пример нескольких мер, позволяющих в сплетениях связей выделить самые важные.

Как вы понимаете, характер образования связей в сетях - не случаен. Особенно - в социальных.

Первым, кто обратил внимание на то, как информация о, например открывшихся вакансиях, распространяется среди людей, был Грановеттер. Ещё в 70-х годах прошлого века он заметил, что большая часть общения у людей происходит в небольшом тесном кругу близких друзей, при этом самая интересная информация о новых возможностях, как правило, происходила от случайных знакомых.

Коэффициент кластеризации [13] - мера связности окружения отдельной вершины - количество связей между соседями, поделенное на максимально возможное число рёбер (для n соседей \[ E_{max} = n(n-1)/2 \] в случае неориентированного графа).

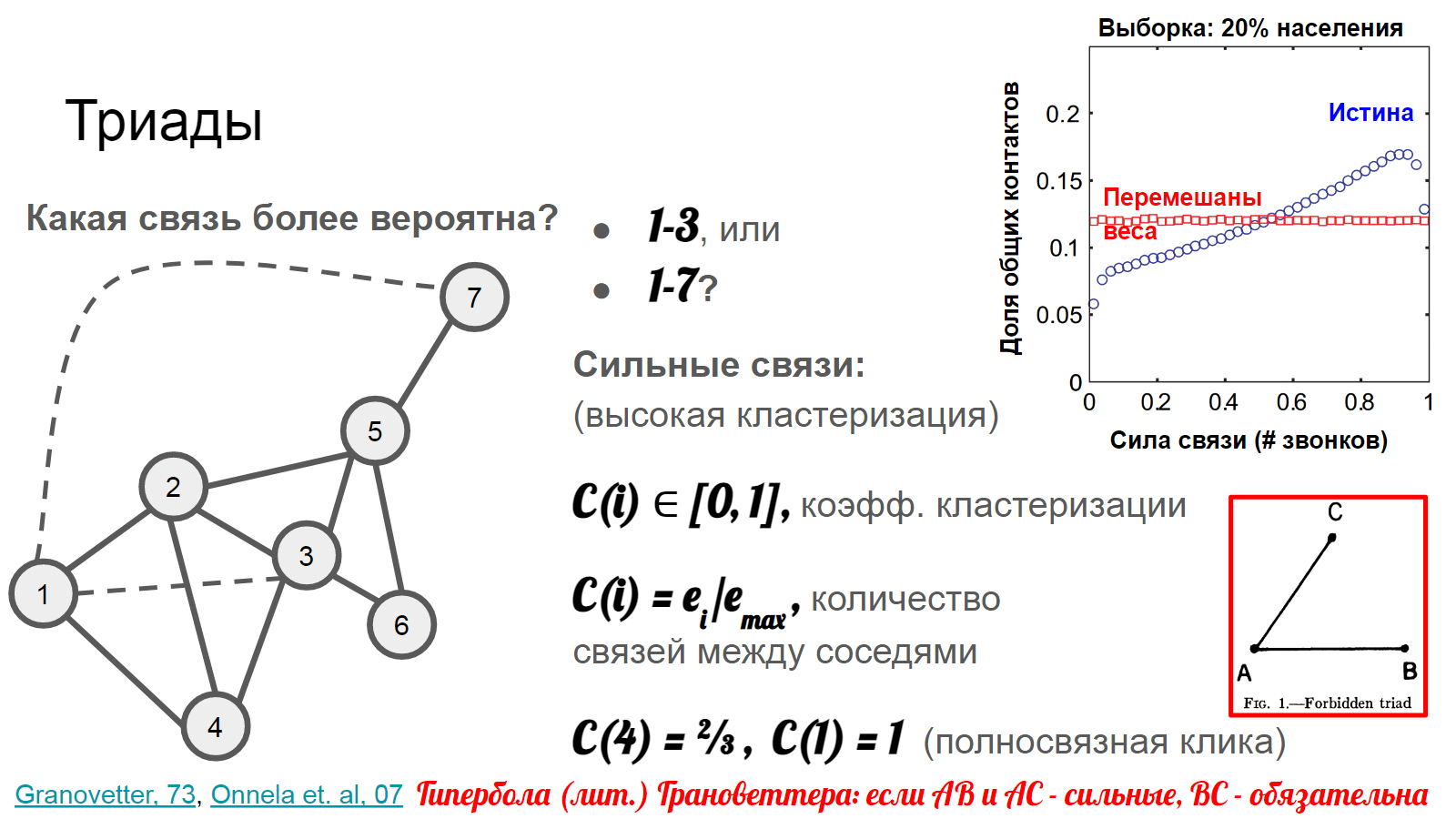
Например, для вершины #1, у которой все соседние вершины {2,3,4} - связаны между собой - коэффициент кластеризации будет единица.

В то же время, у вершины #4 - не все соседи связаны и коэффициент будет равен ⅔.

Грановеттер предположил [14], что невозможен треугольник, такой, что АВ и АС - сильные связи (много общих знакомых), а ВС - отсутствует.

То есть, если А дружит с В и у них много пересекающихся контактов, и то же самое верно про А и С, то просто невероятно, что они не будут знакомы - преувеличение, но незначительное. Гипотеза дождалась проверки в наше время, когда данные контактов между людьми стали доступны на уровне популяции - благодаря распространению мобильной связи.

Так в 2007 один из европейских операторов, обслуживающий 20% населения страны, проанализировал частоту и звонком между всеми абонентами. И выяснилось, что всё верно заметил Грановеттер - чем больше у пары абонентов общих контактов, тем чаще они общаются [15].

В ориентированном графе треугольники бывают разные. Собственно, для трёх вершин существует 13 способов связности. И в природе мы наблюдаем повторяющиеся структуры высшего порядка (состоящие из нескольких вершин). И частота их появления значительно отличается от случайной. Такие структуры называют мотивами [16].

Они встречаются в пищевых цепочках, связях нейронов в мозгу, рисунке транспортной сети, электрических схемах, финансовых транзакциях, и социальных взаимодействия. Выявление таких структур позволяет оценивать структурные блоки, которые организовывают сложные системы. Как правило, в различных системах - различаются частоты появления отдельных видов микроструктур и это позволяет строить профиль значимости мотивов - частоты их образования - для различных сетей и делать выводы о принципах их организации.

Например, этот подход позволяет сравнить морскую экосистему и потоки пассажирского транспорта.

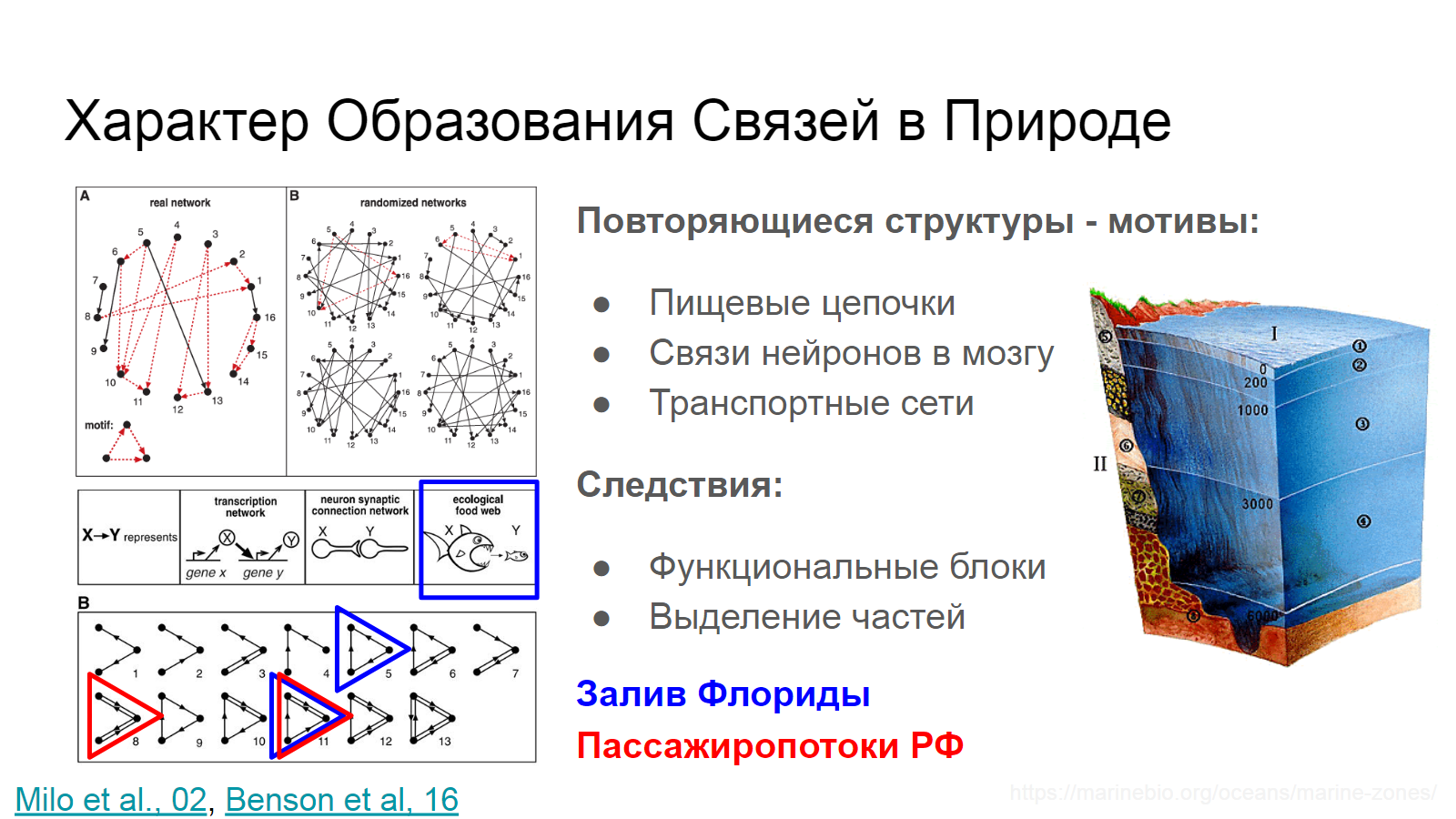
Во глубине флоридских вод обитает большое разнообразие всякой живности, которая постоянно обменивается питательными веществами. Ну как обменивается - кто кого догнал, тот себе веществ и выменял - по такому принципу строится граф обмена углеродом (пищевая цепочка). Учёт мотивов позволяет разделить граф на кластеры [17], соответствующие вертикальным слоям - ареалам обитания живности - весьма точно. При этом модель не знает ничего об особенностях отдельных вершин - лишь стремится разложить их по полочкам так, чтобы количество мотивов в каждом кластере было максимальным. И этот метод спектральной кластеризации мотивов позволяет добиться весьма качественного разделения всей экосистемы на составные части.

Не все вершины одинаково популярны.

Зададимся вопросом. Какова p(k) - функция распределения количества связей k у вершины графа? Думаете, гауссиана? Собственно, именно нормальное распределение степеней мы ожидаем для случайного характера соединения (эту модель в середине прошлого века предложили Эрдош и Рейни [18]). На самом деле, связи-то образуются неслучайно и в природе не только нет прямых линий, но и регулярные структуры отношений - редкость.

Первым, обратившим внимание на неравномерное распределение личного богатства среди граждан, был итальянский экономист Вильгельмо Парето [19]. Наверняка вы слышали о правиле 80/20 - 20% усилий приносят 80% результата - так можно выразить принцип минимальных усилий, встречающийся сплошь и рядом.

В общем виде такая статистическая зависимость задаётся степенной функцией распределения \[ p(k) = k^{-\alpha} \] (и её вариациями, вроде закона Ципфа [20], принимающего во внимание не количество связей, но ранг - порядок очерёдности размера в системе - например, частота самого употребляемого слова в два раза выше частоты следующего по популярности, или же в экономике потребления - размер доли лидера рынка в два раза больше доли ближайшего конкурента, и в четыре - доли следующего в списке).

В розничной торговле тот факт, что не все продукты одинаково популярны, приводит к тому, что мы наблюдаем как Амазон, имеющий возможность предложить покупателю огромный ассортимент, теснит традиционных лавочников, торгующих лишь самым популярным ассортиментом. Длинный хвост продаж, состоящий из большого числа не самых популярных товаров, позволяет им собирать значительное количество заказов и привлекать всё больше клиентов.

Многие события в природе руководствуются ленью [21] - мне вспоминаются слова тренера по гребле о том, что правильная техника нарабатывается только в состоянии близком к истощению - тело находит оптимальное движение, экономящее усилия.

Вопросом о том, кто же в системе - самый социологи задаются уже давно. И способов определения самости - мер центральности [22] придумано уже немало. Важно помнить о том, что когда мы слышим, что решение оптимально, то хорошо бы уточнить - а по какому критерию.

Диффузия | 33-35

С кем поведёшься - от того и наберёшься, говорят в народе. Рассмотрим процесс распространения информации в сети и приведём несколько исторических примеров: про индейцев, оленеводов и парусники.

Эпидемии и их динамика - популярная сейчас тема. Важно понимать, что хотя сам факт заражения и болезни - биологические процессы борьбы организмов за ресурсы и адаптации к изменчивой среде, эпидемия - явление социальное [23].

Важные особенности этого процесса. Во-первых, заражение передаётся через социальные (и около-социальные, вроде использования общественного пространства или транспорта) контакты. Парадокс друзей состоит в том, что у ваших друзей - больше друзей, чем у вас самих. Из-за того, что социальная популярность неравномерна - хабы (наиболее тесно связанные или центральные узлы) оказываются:

(а) подвержены риску заражения больше других, (б) представляют собой угрозу распространения ифекции (в невыявленной стадии).

Представьте, мы моделируем случайный процесс заражения, выбирая пострадавших подбрасыванием монетки. Если рассматривать вершины как несвязанные между собой точки, то и шансы у всех будут равные. В реальном мире заражение передаётся через контакт, поэтому модель выборки путей передачи из множества рёбер - более адекватно описывает процесс. И из-за того, что у некоторых вершин больше всего связей - именно они оказываются в группе риска.

Как показал ретроспективный анализ распространения предыдущих эпидемий (SARS, Эбола, чума в Средневековье), зараза имеет свойство путешествовать вместе с транспортными потоками. Поэтому наиболее точными моделями, предсказывающими динамику развития ситуации на сегодняшний день являются иерархические метамодели [24]- учитывающие связи групп (социальные и транспортные).

Кроме заразы в сетях распространяются идеи и убеждения. Здесь мы сталкиваемся с эффектами социального давления и личной выгоды, моделировать которые позволяет теория игр. Подобные процессы называются каскадами принятия решений (в то время как эпидемии не зависят от решений, заражение ведь - воля случая, и называются вероятностными каскадами).

Рассмотрим пример распространения новой технологии, скажем, средства обмена сообщениями. Подобное - притягивается и мы часто разделяем привычки и взгляды друзей. Рассмотрим стратегию выбора - использовать новый инструмент общения или не использовать. Пусть каждый из участников рассматриваемой сети руководствуется рациональным правилом - начинает использовать новое средство общения если более половины контактов им пользуются.

Динамика распространения нововведений зависит от структуры связей.

Одним из первых исследователей социального характера распространения нововведений, был Эверетт Роджерс. Его труд “Diffusion of Innovations”, выдержавший пять прижизненных изданий с 1962 по 2003, является основой для всех современных методологий проведения организационных изменений.

Ещё во время работы над первой версией теории автор обратил внимание на то, что группы адептов инноваций различаются как по своим социально-экономическим характеристикам, так и по мотивам, движущим принятием решения о использовании новинки.

Инноваторы составляют малочисленную группу азартных искателей приключений - их связи космополитичны, стиль жизни - не всегда одобряем местным обществом, уровень образования - должен быть достаточным для понимания сложных вещей раньше прочих, достаток - позволяет проводить эксперименты, через них нововведения попадают в локальные системы.

Ранние пользователи - напротив, столпы общества, респектабельны и хорошо интегрированы на локальном уровне, к ним обращаются за советом и их пример является знаком одобрения инновации для прочих, их роль - стать триггером накопления критической массы новых практик в системе.

Третья группа - сознательные граждане - раннее большинство, достаточно хорошо интегрированы в местные связи, руководствуются выгодой, держат нос по ветру, благодаря им система насыщается новизной до половины и это становится точкой, когда начинается лавинообразный рост.

Позднее большинство - скептически настроенные товарищи - такие не пошевелятся, пока большинство знакомых не начнут, обычно обладают ограниченными ресурсами и должны убедиться в том, что соседи убедились в надёжности новинки.

В последнюю очередь инновации доходят до социально изолированных маргинальных групп, очень традиционных в своих воззрениях (могут высказывать мнение: “Так делалось всегда!”) и считающих сопротивление переменам рациональным выбором, обыкновенно наименее образованные и экономически свободные граждане.

Во многих социальных системах наблюдается свойство гомофилии [25] - подобное притягивается. И это зачастую становится барьером на пути распространения нового - прислушиваются ведь преимущественно к мнению “своих”, а к “чужакам” - относятся подозрительно или даже враждебно.

Разделение групп по цвету кожи, месту проживания и прочим социально-экономическим характеристикам - весьма распространено среди людей. Внутри групп зачастую существует своеобразный культурный код (это может быть жаргон или система взглядов, примеры - панки, врачи, моряки торгового флота). Учитывать такие особенности - важно.

Не все инновации распространяются одинаково.

Например, такая очевидная вещь, как использование кипячёной воды - не смогла прижиться в перуанской деревне, т.к. их система взглядов не позволяла принять факт того, что в случае желудочных расстройств нужно использовать обеззараженную воду, а в существование бактерий поверить граждане-индейцы не смогли.

Вообще, неконтролируемые и непродуманные инновации могут наносить ощутимый вред самобытным культурам. Например, так мотосани разрушили быт и общественный уклад лапландских оленеводов, которые стали забивать оленей, чтобы обслуживать технику.

Ещё один показательный случай - голод в Ирландии - результат цепочки инноваций. Сначала из Нового Света привезли картофель - и он победно занял доминирующую нишу в сельском хозяйстве и рационе добрых католиков. Затем пришла беда - из того же Нового Света привезли паразита - грибок, уничтожавший картошку подчистую. Причина оказалась в том, что ранее между континентами курсировали суда старого образца, и заражённые грибком корнеплоды спокойно себе сгнивали в трюмах во время долгого пути. С изобретением клиперов вояж стал быстрее и интереснее. И пара картофелин-таки уцелела. Принеся в Ирландию новую форму жизни, ставшую причиной весьма грустных событий. Поэтому, всякий раз, внедряя или планируя инновации, хорошо бы подумать о последствиях.

Наконец, важное наблюдение - если кто будет работать в системных интеграторах и окажется перед соблазном действовать через инноваторов в клиентской организации, то мой вам совет - обращайте свои усилия на столпов общества - это повысит ваши шансы на успех.

■ Прикладные задачи

Машинное обучение | 36-41

Коротко о самых известных задачах, которые можно решать на графах. Область растёт, количество приложений прирастает с каждой конференцией. Добро пожаловать в сингулярность. Объять необъятное даже пытаться не будем.

А вот задачу предсказания связи - рассмотрим детально.

Пожалуй, самой известной задачей является нахождение сообществ (она же кластеризация графа [26] - не спутайте с классической задачей кластеризации [27]) - мы предполагаем, что в системе есть множества сущностей связанных между собой теснее, чем с остальными и стремимся разделить граф на части таким образом, чтобы максимизировать связность внутри частей. Задача сама по себе непростая, т.к. не всегда просто определить однозначно принадлежность к какому-то сообществу, да и сообщества в реальности могут пересекаться. Есть много интересных алгоритмических решений, не все из них имеют математические гарантии. Самые популярные эвристики - вроде метода Гирван-Ньюмана [28] или лидирующего по популярности алгоритма Louvain [29] вообще родом из физической части сообщества специалистов по сетям. В общем, во всех этих методах мы стремимся найти оптимальное сечение графа, максимизирующее его модулярность (мера качества разделения).

Как мы уже знаем, не все вершины связаны одинаково. Некоторые из них - соединяют сообщества. Tак, например, потоки информации между отделами в традиционных компаниях протекают через формальное руководство, да неформальных лидеров, знающих входы и выходы [30] [31].

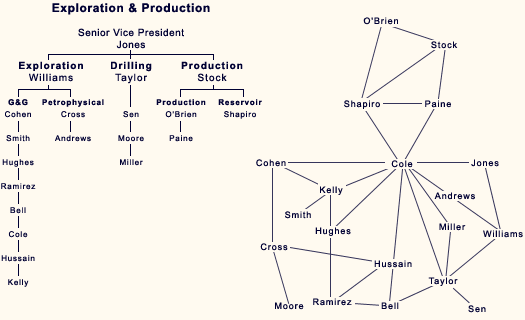
Характер связности вершины определяет её роль в системе [32]. Так, например, в масштабном исследовании [33] проведения организационных изменений в английских больницах выяснилось, что наиболее успешными были агенты изменений, обладавшие разветвлённой сетью контактов. У них получалось договориться со всеми по-отдельности, а вот тем, чьи контакты были тесно знакомы между собой - нелегко пришлось, т.к. публика против перемен объединялась. Сейчас у нас есть алгоритмы, позволяющие решить вопросы выявления групп и ролей в сетях достаточно эффективно. Стоит заметить, что графовые нейронные сети очень здорово показывают себя в данной группе задач.

Следующая задача машинного обучения - классификиция. Причём, решать её мы можем как для вершин, так и для графов (и для рёбер тоже). Вопросами в данном случае будут: “Вот у нас есть молекула, а что это за элемент в её структуре?”, или “Вот эта молекула - яд или лекарство?”, “Как будет между двумя молекулами реакция протекать?”.

Все эти вопросы имеют большое практическое значение в химии, материаловедении, фармакологии и многих других интересных областях хозяйства, вроде виноделия и кулинарии.

Наконец, задача которую мы рассмотрим в деталях - предсказание связи [34].

Пусть у нас есть граф, заданный на неком временном интервале. Обозначим его G[t0, t’0].

Мы будем пытаться создать ранжированный список L связей (изначально отсутствующих в G[t0, t’0]), которые появятся в этом же самом графе G[t1, t’1] в другой момент времени. Отобразим данное множество предполагаемых связей на рисунке красным пунктиром.

Оценка качества прогноза происходит следующим образом: пусть n = |Enew| - количество связей G[t1, t’1], появившихся в нашем графе. Берём первые n элементов L и считаем совпадения.

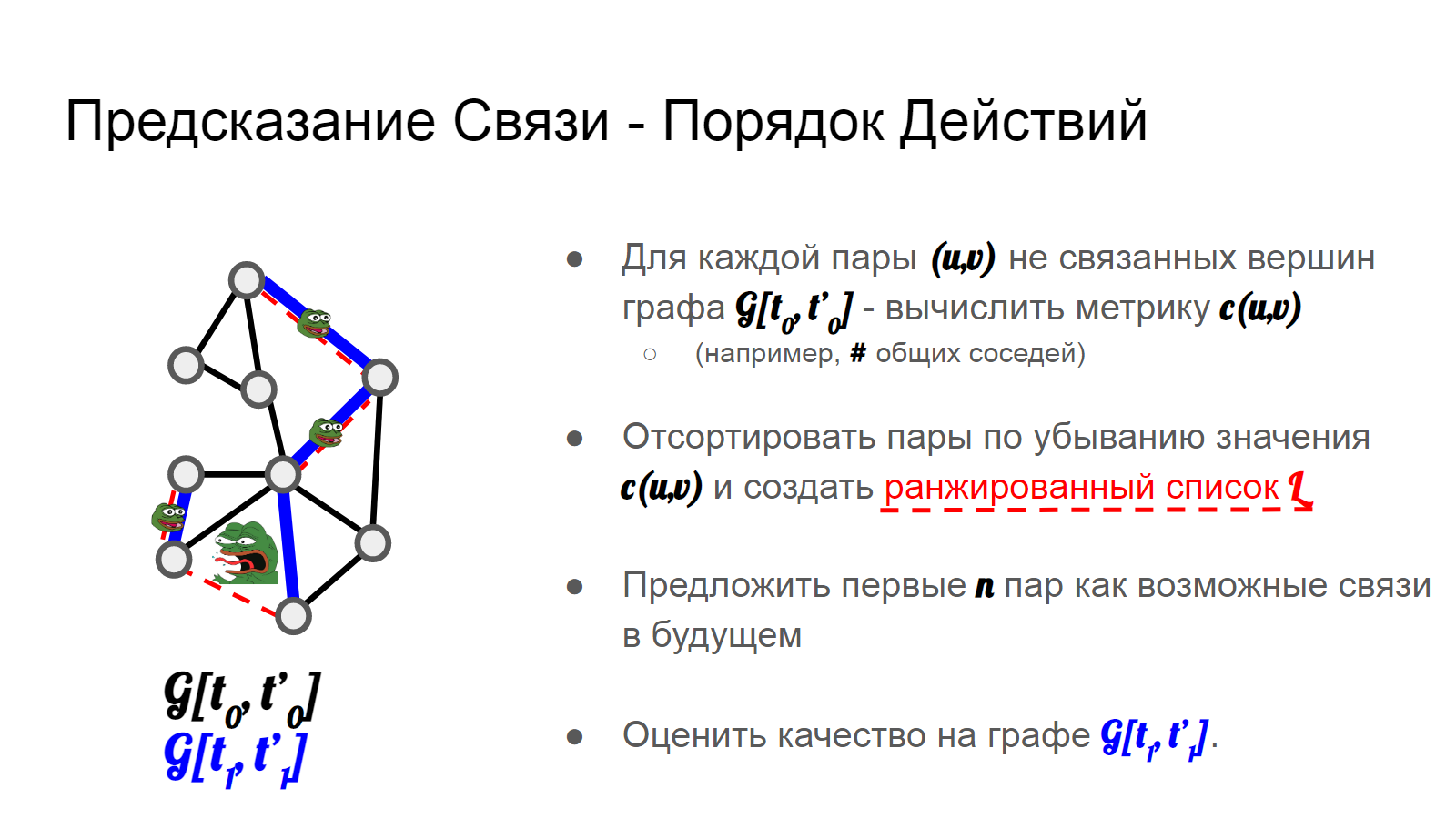
Пепе счастлив, когда наш прогноз верен. Хорошо бы делать так почаще.

Порядок действий - следующий. Для каждой пары (u,v) не связанных вершин графа G[t0, t’0] - необходимо вычислить некую метрику c(u,v). Например, вспомним заветы Грановеттера и посчитаем количество общих соседей. Далее - отсортируем пары по убыванию значения c(u,v) и предложим первые n из них как возможные связи в будущем. Оценим качество на графе G[t1, t’1].

Стандартный список методов, которые уже проявили себя хорошо: (1) Геодезическая дистанция: 1 / h u,v - чем вершины ближе на графе, тем больше шансов, что между ними возникнет связь [35].

Отметим пару вершин. U - синим. V - красным.

Как видите, они всего в двух шагах. Даже окружение у них частично пересекается.

(2) Общие соседи: |Γ(u) ∩ Γ(v)| - чем больше общих соседей, тем сильнее связь, как это подметил Грановеттер.

(3) Жаккардов индекс: |Γ(u) ∩ Γ(v)| / |Γ(u) ∪ Γ(v)| - чем большая доля соседей - общие, тем выше шансы образования связи в будущем [36].

(4) Адамик/Адар: ∑z∈ Γ(u) ∩Γ(v) 1/log |Γ(z)| - нормализуем вышесказанное логарифмом количества связей каждой вершины, входящей в множество общих соседей [37].

(5) Предпочтительное присоединение: |Γ (u)| ⋅ |Γ(v)| - чем больше у вершины рёбер, тем больше шанс пересечься с другой вершиной, у которой тоже много рёбер [38].

(6) PageRank: [ r_u(v) + r_v(u) ] - шанс того, что случайное блуждание из одной вершины, приведёт к другой.

PageRank | 42-47 *

Казалось бы, к чему здесь Эдита Пьеха?

Рассмотрим детальнее работу PageRank - алгоритма ранжирования вершин, определившего успех компании Google [39].

Дело было в конце прошлого века, интернет тогда был поменьше, чем сейчас, но разобраться в 200+ М страниц уже было непросто и многие стремились всю эту массу информации как-то по полочкам разложить. Вопрос как ранжировать результаты поиска по их релевантности запросу - актуален и по сей день.

Сергей Брин и Ларри Пейдж в то время были аспирантами в Стенфорде и их идея отличалась от традиционного подхода. В общем, они предложили вместо анализа содержимого страниц обращать внимание на то, как эти страницы между собой связаны. Идея в том, что на качественную страницу - многие ссылаются. И чем больше у страницы входящих гиперссылок, тем она лучше. А если среди ссылающихся на неё источников - есть и другие популярные, то она ещё лучше.

Математически это можно выразить как некое равновесие ограниченного ресурса в системе, который перераспределяется между страницами в зависимости от того, на кого они ссылаются и кто ссылается на них.

Ранг каждой страницы определяется как сумма долей ранга каждой ссылающейся на неё страницы, причём эта доля - соответствует рангу ссылающейся страницы, разделенному между теми, на кого она ссылается. Как поёт Эдита Пьеха, кто-то находит, кто-то теряет [40].

Как этот ранг вычислить? Всё просто - достаточно определить структуру связей, разделить некое количество ресурса между вершинами (обыкновенно - поровну) и начать процесс перераспределения благ по обозначенной формуле. С каждым тактом времени в системе мы будем высчитывать значение PageRank для каждой вершины как перетекание доли PageRank от всех вершин, ссылающихся на неё.

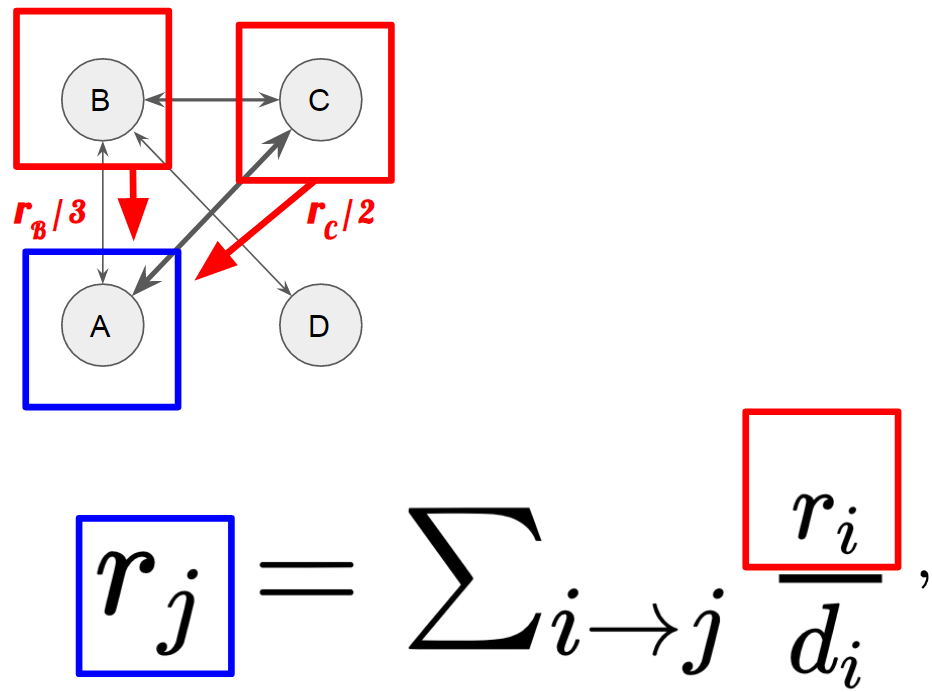
Так в вершину A перетечёт треть PageRank вершины B, а от вершины С - половина.

Повторим вычисление для остальных вершин.

Чем-то это напоминает игру в Монополию, когда ресурсы перераспределяются между участниками системы в зависимости от того, кому принадлежат клетки игрового поля, по которому согласно выброшенной комбинации игральных костей передвигаются фишки.

Мы можем и будем хранить значения PageRank для отдельных вершин в векторе и это позволит переписать сумму как произведение матрицы на вектор.

Для этого нам потребуется выразить граф в виде матрицы. Сначала мы создадим матрицу связности A, ненулевые элементы которой соответствуют наличию связи между вершинами. В общем виде мы можем оперировать весами рёбер, а частным случаем является бинарная матрица связности, элементы которой могут принимать значения 0 и 1.

Из матрицы связности A мы можем сформировать матрицу переходов между вершинами M, т.н. столбцовую стохастическую матрицу, столбцы которой в сумме дают 1.

Эта матрица задаёт случайное блуждание - марковский процесс [41] первого порядка, в котором каждое следующее положение определяется только текущим положением (вершиной, в которой находится бродяга).

Уравнения - как через суммы, так и в матричной форме - оба решаются итеративно и обычно достаточно 30-50 итераций (поочерёдного перетекания PageRank между вершинами, либо перемножений матрицы на вектор) для стабилизации значений. Собственно, PageRank - вероятность нахождения бродяги в отдельной вершине (т.н. стационарное распределение случайного блуждания).

Подобная “ванильная” формулировка, впрочем, подвержена двум рискам:

(1) тупики - если в графе есть вершины только с входящими рёбрами, то через них PageRank будет “утекать” из системы и вектор заполнится нулями (а бродяга - застревать, т.к. идти ему будет некуда) и

(2) паучьи гнёзда - вершины, ссылающееся на себя (как это делают некоторые учёные мужи, занимающиеся самоцитированием) - они будут аккумулировать PageRank, постепенно забирая его весь из системы (а бродяга - будет бродить кругами).

Во избежание этих бед Брин с Пейджем выдали бродяге телепорт.

То есть теперь бродяга всякий раз, придя в очередную вершину, будет либо совершать шаг в направлении одного из исходящих рёбер, либо телепортироваться в случайно выбранную вершину (обычно с вероятностью Beta ~1/7). Из тупиков - всегда телепортируется. Перезаписав с учётом фактора телепорта матрицу переходов, мы можем решить задачу выявления самых популярных страниц качественнее.

Внимание, данная формулировка всё ещё чувствительна к тупикам, через которые PageRank утекает из системы (убедиться в этом вам поможет домашнее задание, в котором предлагается реализовать вычисление PageRank) и одним из способов борьбы с данным явлением будет просто доливать утекшее после каждого такта.

Персональный PageRank и сравнение методов в задаче предсказания связи | 48-49 **

Вскользь - об одном из самых важных алгоритмов за минувшие 20 лет (личное мнение) и важности использования простых моделей.

Усложним задачу. Пусть бродяга телепортируется не в случайно выбранную, а одну из заранее определённых вершин.

Для этого ещё раз модифицируем матрицу переходов.

Такой подход называется персонализированный PageRank [42] - мы получаем стационарное распределение вероятности посещения вершин относительно некоего стартового множества. И это позволяет готовить весьма качественные рекомендации (как это, например делают в Pinterest и Одноклассниках) https://habr.com/ru/company/odnoklassniki/blog/499192/

А если это множество стартовых вершин состоит из одной вершины, то мы получаем случайное блуждание с рестартами, которое и позволяет решить вопрос прогнозирования связи между двумя вершинами.

Рассмотренные методы задают базовый уровень качества и работают в среднем в 30 раз лучше подбрасывания монеты. Поэтому, если вы вдруг зададитесь целью построить новую систему рекомендаций - обязательно используйте эти простые методы в качестве базы для сравнения. Если натренированная нейросеть выдаёт качество прогноза хуже, чем дистанция Адамик/Адар, то скорее всего есть потенциал для улучшения.

Векторные представления графов | 50-58

Современная тенденция, здесь речь пойдёт о методах, основанных на случайных блужданиях. В качестве дополнительного материала рекомендую ознакомиться с докладом о текущем состоянии дел [43] от автора одной из самых выразительных моделей современности.

Историю появления теории графов в трёх словах можно записать как “Эйлер. Мосты. Лень”. Так, собственно и случилось. Приехал он как-то в Питер, там кто-то подкинул ему задачу про мосты, что сейчас стоят в Калининграде. Задача была нерешаемой и выдающийся математик, член Петербургской академии наук, вместо того чтобы её решать и почём зря голову сушить, придумал матаппарат, показывающий принципиальную невозможность решения головоломки.

Так и мы, вдохновившись примером одного из величайших умов, будем лениться. Перестанем выдумывать все эти эвристики, описывающие вершины, и посмотрим в сторону векторных представлений. В общем, задачей становится поиск функции отображения вершин графа в векторное пространство некой размерности.

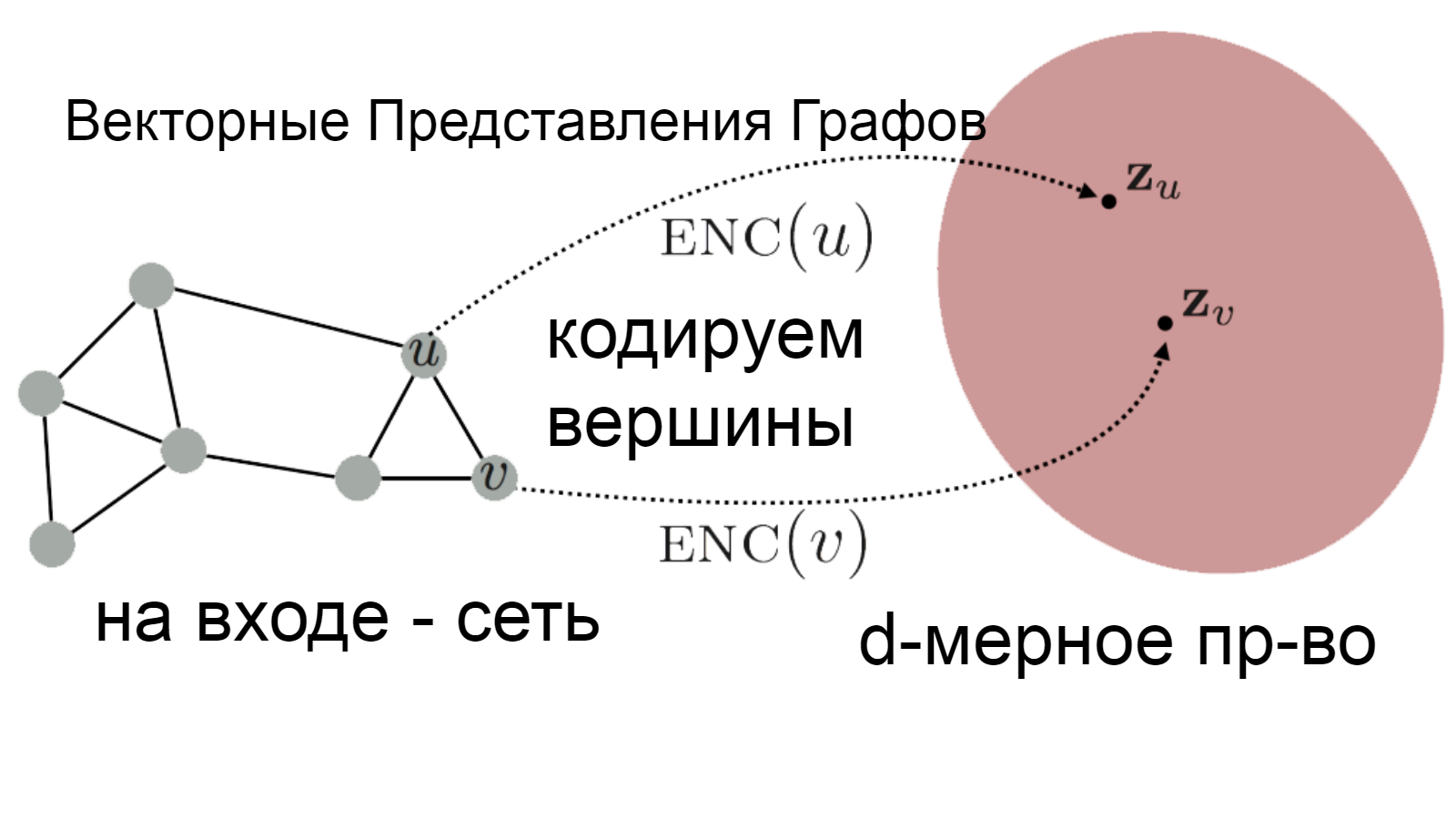
То есть, мы берём сеть, подаём её на вход некой параметрической функции-энкодера, на выходе получаем векторные представления. Задача оптимизации сводится к тому, чтобы подобрать параметры энкодера таким образом, чтобы смежные вершины отображались похожими векторами. То есть, чтобы угол между ними был минимальным.

И в простейшем случае функция потерь, позволяющая оценить качество параметров энкодера, задаётся матрицей связности.

Посмотрим на вопрос шире. Матрица связности позволяет определить функцию потерь для непосредственных связей вершины. Но ведь есть ещё соседи соседей. И соседи соседей соседей. Как бы так учесть более широкий контекст связности вершины?

Внезапно мы вспоминаем, что частота связей вершин чем-то напоминает частоту слов в человеческом языке.

На улице 2014 год, все уже прослышали про недавний успех языковой модели word2vec [44] образца 2013. Проверяем статистическую гипотезу - слово в предложении определяется контекстом - на графах. Для этого запускаем короткие случайные блуждания по графу и обучаем на них word2vec, оптимизируя параметры модели таким образом, чтобы вершины, встречающиеся на пути бродяги, были расположены близко в векторном пространстве.

Функция потерь задаётся логарифмом вероятности нахождения двух вершин на одном пути.

Эта идея сработала. Первым проектом был DeepWalk [45], в котором бродяга перемещается по графу хаотически. Развитие мысль о блужданиях получила в алгоритме node2vec [46], в котором характер движения бродяги задаётся дополнительными параметрами. Оба метода - используют одну и ту же однослойную нейронную сеть. И в результате обучения модель представляет собой таблицу соответствия вершина-вектор. Из-за того, что оптимизируем мы вероятность нахождения двух вершин на одном пути, эти методы сходятся к Personal PageRank.

Достаточно продолжительное время внимание исследователей было направлено на разработку стратегий движения бродяги. Следующий качественный скачок эволюции методов оказался в соседней области.

В проекте VERSE [47] авторы задались целью оптимизировать распределение вероятностей появления вершин на пути бродяги. И это позволило одной модели стать настолько выразительной, что она может распознать сообщества, общую структуру сети, и локальные роли вершин. SOTA в задаче предсказания связи и заслуженные аплодисменты от преподобного Байеса.

Здесь внимательный слушатель и читатель задастся вопросом - а почему это речь всё время идёт о свойствах и векторных представлениях вершин, когда мы вроде как разбираем задачу предсказания связи? Как готовить представления для рёбер?

Всё просто - возьмём два вектора вершин и тензорно их умножим. Или сложим. Ещё можно усреднить. Или посчитать дистанцию - минковского или эвклидову. А то и просто рядом поставить (конкатенировать). Особенно устойчиво в экспериментах себя показывает тензорное произведение (адамара), но здесь следует упомянуть Free Lunch Theorem [48] и напомнить о том, что в каждой ситуации желательно протестировать несколько методов - это повысит шансы нахождения (суб)оптимального решения.

Глубинное обучение | 59-64

Здесь мы рассмотрим механику работы свёртки графа. Бытует мнение о том, что царских путей к геометрии не бывает, но это не точно. Вскользь рассмотрим один из вариантов реализации графовой нейронной сети, предложенный несколько лет назад аспирантом из Амстердама и наделавший шуму в научном сообществе благодаря исключительной простоте реализации.

Недостатком методов, основанных на неглубоком обучении является трансдуктивность - модель единоразово выучивает векторные представления для вершин и всякий раз при изменении графа её необходимо переучивать. Кроме того, из-за того, что входные данные для модели получаются в результате случайных блужданий, полученные представления всякий раз будут различаться (если мы не зафиксируем сид - стартовый параметр генератора псевдо-случайных последовательностей). Для их совмещения потребуется совершать поворот пространства, как это сделали в проекте MUSE от фейсбук. Идея была в том, чтобы совместить векторные представления для различных языков по координатам общеупотребляемых слов, вроде “президент”. Дело это непростое, и не ко всем приложениям применимое.

От обозначенных недостатков свободны глубокие модели - графовые нейронные сети.

Идея, в общем-то простая - раз граф - данные без чётко заданной размерности и порядка (см. изоморфизм) и подать их в обычную нейронную сеть не получится (кстати, о графовых свёрточных сетях в деталях рассказывает следующая лекция, материалами для которой поделились коллеги из Стенфорда, ведущие замечательный курс cs224w о машинном обучении на графах, материалы которого доступны для самостоятельного страдания всем желающим), то попробуем нейронную сеть уместить в имеющийся граф [49].

Идея в том, что для каждой вершины мы строим вычислительный граф. Запускаем случайное блуждание на k шагов от этой вершины. Так мы задаём окружение - выборку, свойства которой влияют на нашу вершину. Как говорят в народе - скажи мне, кто твой друг и я скажу, кто ты. И затем собираем свойства её соседей через нелинейные аггрегаторы (те самые нейронные сети), параметры которых являются общими для всего графа.

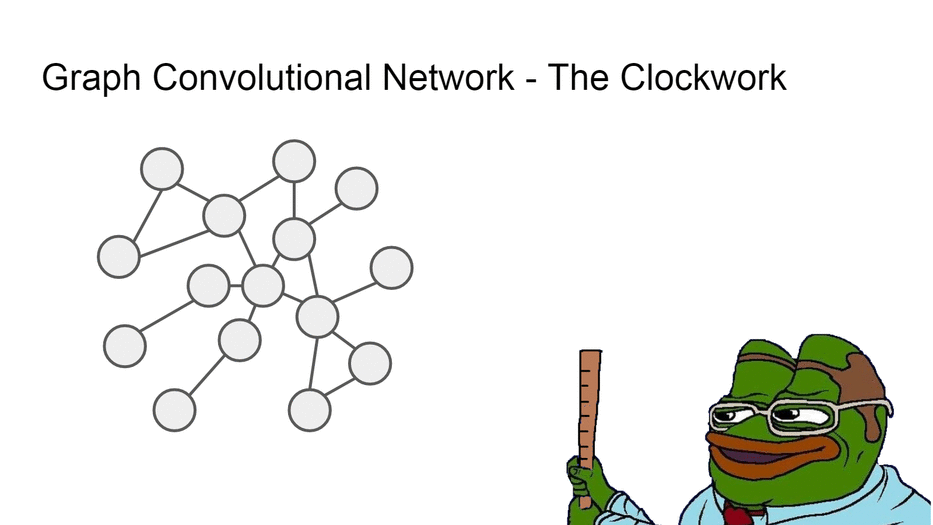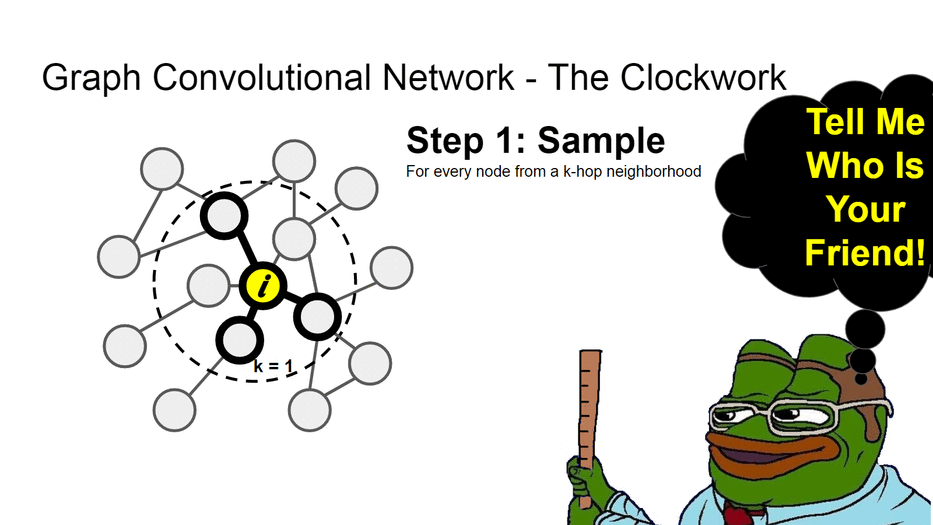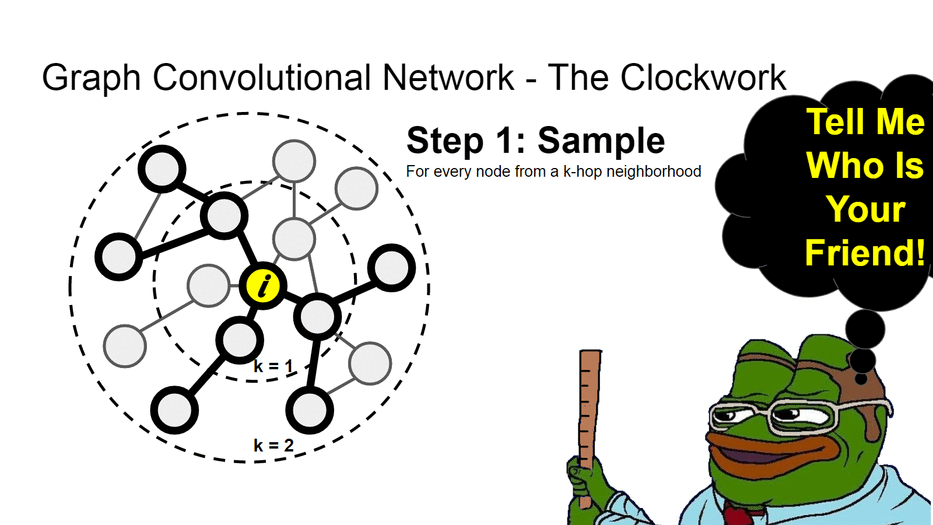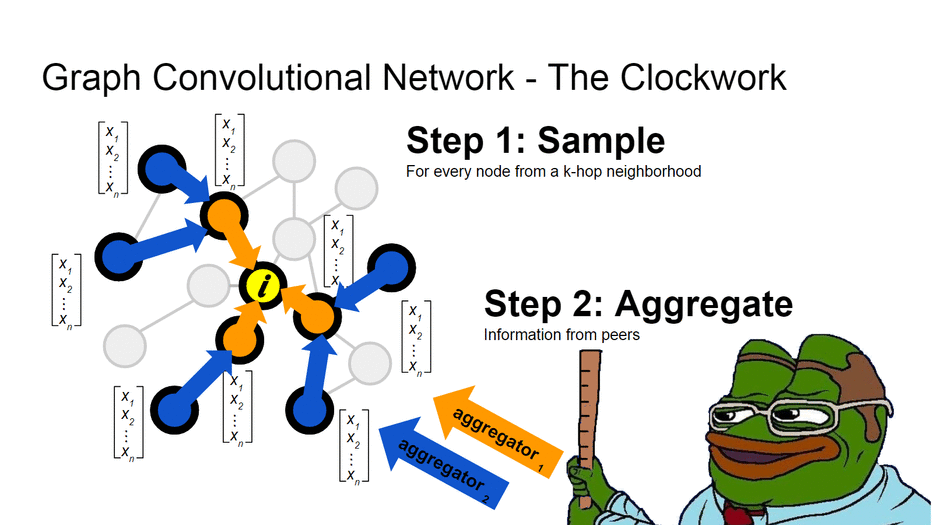
У нас будет отдельная лекция по этим архитектурам, поэтому сейчас - рассмотрим базовые принципы работы графовых свёрточных сетей.

Аггрегаторы - нелинейные функции, желательно - дифференцируемые. Работают они в два шага: первым делом собирают информацию о соседях, а затем - комбинируют (зачастую это просто конкатенация, но могут быть) с имеющейся информацией о вершине [50].

Одним из вариантов подобной аггрегации является перемножение матрицы связности, вернее, её нормализованного лапласиана на матрицу свойств [51].

Эта операция моделирует потоки между вершинами, и в общем-то большинство современных графовых нейронных сетей - так и функционируют.

Правило для сигнала каждого слоя принимает вид.

Данный способ требует держать матрицу связности в памяти, что может быть накладно для больших графов. Работающие же с сетями среднего и малого размера апплодируют данному методу. Простота реализации (сама операция аггрегации - три строки) вызвала нешуточное оживление интереса к графам среди исследователей машинного обучения и даже вызвала хайп и волну последующих публикаций. Рекомендую, красивая модель, использую её в качестве базовой.

Современные тенденции | 65-67

Вскользь - о паре значимых для отрасли работ: предобучение графовых нейронных сетей и поиск приблизительных (и весьма точных!) ответов на непростые вопросы на пересечениях многомерных фигур. Можно сказать, что это - в каком-то смысле отсылка к наследию Казимира Малевича, но это, как вы понимаете, разумеется не точно.

Тут стоит отметить пару работ - первая о стратегии предобучения графовых свёрточных сетей [52]. Здесь мы вспоминаем о том, что можно выделить контекст - структуры, окружающие вершину. Поступаем творчески - сначала задаём некое окружение для вершины (BFS на k шагов). Затем - выделяем центральную структуру и структуры, вокруг центральной. Все их - кодируем в вектора с помощью графовой свёрточной сети. Далее, приступаем ко второму этапу - маскируем вершины и учим ещё одну GNN их угадывать. Комбинируем оба подхода и в результате можем предобучать и дообучать сети в ситуациях когда общих данных (вроде базовых химических взаимодействий) - достаточно в открытом или коммерческом доступе, а специфические (вроде определённых реакций - собирать долго и дорого. Любители работы с текстами здесь увидят что-то похожее на BERT. Самое время напомнить, что трансформеры - частный случай графовых сеток - Graph Attention (GAT) [53].

Ещё одна тенденция - искать ответы на вопросы как пересечения множеств гиперпространств [54]. Вот есть у нас граф знаний, в котором связаны концепции. И есть вопрос. Проецируем сущности в вектора таким образом, что связи между концепциями помещаются в гиперпрямоугольники. И находим ответ как геометрическое место точек на пересечении этих фигур. То есть скрещиваем в каком-то смысле буллеву алгебру с гипергеометрией. Возникает вопрос: а что, так можно было? Почему бы и нет!

Говоря о современниках - авторы представили улучшенную и расширенную модель (теперь поддерживается логическое отрицание) пару недель назад - отрадно наблюдать движение прогресса [55].

Космические корабли и всё такое | 68-75

Вернёмся из гиперпространства к делам земным и поговорим об истории космонавтики, здоровом питании и важности обеспечения качества продукции. Посмотрим, как именно современные достижения теории графов позволяют описать производство и решить задачи выходного контроля и разбора полётов.

А теперь, как и обещал, поговорим о космических кораблях и всём таком.

В конце прошлого тысячелетия, когда я учился на первом курсе в киевском политехе, у нас был замечательный предмет - история развития авиации и космонавтики. Неспроста был, так как моя alma mater - Кафедра Телекоммуникаций Факультета Авиационных и Космических Систем (ныне - отдельный Институт Телекоммуникационных Систем на правах факультета) и полезно знать не только современные тенденции, но понимать как мы ко всему этому пришли.

Когда мы говорим “космонавтика”, то, полагаю, у многих в голове возникает образ улыбающегося Юрия Гагарина и мелькают романтические мысли о том, что работа космонавта - это что-то вроде жизни рок-звёзды: популярность у красивых женщин (вроде Джины Лолабриджиды), встречи с сильными мира сего, даже с августейшими особами, да суровая мужская дружба.

Есть и другая сторона у этой медали.

Жизнь взаперти - непростое испытание, как показал режим самоизоляции. А в ограниченном пространстве - и подавно. Космический корабль - это вам не квартира на 8 квадратных метров. В первые декады освоения космоса командам из нескольких человек по нескольку дней доводилось проводить в пространстве, сравнимом по объёму с автомобилем Жигули.

С естественными потребностями во время орбитальных миссий - то ещё приключение [56].

Одними из первых, кто осознали абсолютную важность безопасности пищи космонавтов были товарищи из NASA, которые разработали протокол Hazard Analysis and Critical Control Points (HACCP) ещё в 60-х во избежание пищевых отравлений на орбите [57]. Спустя 50 лет стандарт является общепринятым, а с 2015 и вовсе закреплён законодательно как обязательный к исполнению на всех предприятиях пищевой промышленности ТС.

Идея протокола в том, что производственный процесс приготовления продуктов питания необходимо описать как серию операций по трансформации ингредиентов и полуфабрикатов в удобоваримый результат. Для каждой операции необходимо определить риски, которые могут повлиять на качество или безопасность продукта. И для контроля рисков - установить меры контроля (вроде критических значений температуры и времени обработки) и способы их проведения. А затем - всё описанное претворить в жизнь.

Вернёмся к Пепе и его производству. Представим, что наш лягушонок сделал верный выбор, разобрался с матричными методами, одолел конкурентов и захватил планету. Теперь перед ним новая задача - освоение космоса.

Как вы помните, Пепе делает пироженки, которые собой представляют секретный ингредиент, расфасованный в вафельные рожки. В плане технологии приготовления - это почти что блин. Вот ссылка [58] на видео процесса производства пустых вафельных рожков.

А если уж вам интересно, откуда такие примеры с вафельками и космосом - всё просто. Мой отец работал техником в советской космической программе и выпекал многослойные печатные платы для электронных компонентов программы Буран. А после этого - какое-то время выпекал вафельные стаканчики, так что мне повезло повидать производство ещё в юности. Кроме того, одним из приключений, которое совершил лично была сертификация систем качества, охраны труда, и заботы об окружающей среде для ведущего мирового производителя сладостей, где мне довелось выступить в роли руководителя всего этого процесса.

Поэтому мы и рассмотрим блин как базовый случай производства продуктов питания с термической обработкой - его можно усложнить, а вот упростить у меня пока ещё не получилось.

Блин тоже граф. Смотрите, почему это так. Чтобы испечь блин, нам потребуются ингредиенты, вроде: сала, яиц, воды, муки и соли. Также не обойтись без оборудования: кастрюли, стакана, ножа, вилки, половника, лопатки и сковороды. Не забудем про ресурсы: тепло и время.

Перейдём к процессу стряпни. Первый шаг - приготовление рассола и это действие состоит из нескольких этапов. Сначала - отмерим воды, для этого потребуется вода, стакан и кастрюля. Затем - подогреем, затратив какое-то количество тепла и времени. Растворим соль, помешивая вилкой. Все эти операции - позволяют установить связи между шагами процесса приготовления, ингредиентами и ресурсами. А зная связи, мы можем записать рецепт в виде графа. Здесь мы будем говорить о связях, не отображая их на рисунке - исключительно ради чистоты картинки.

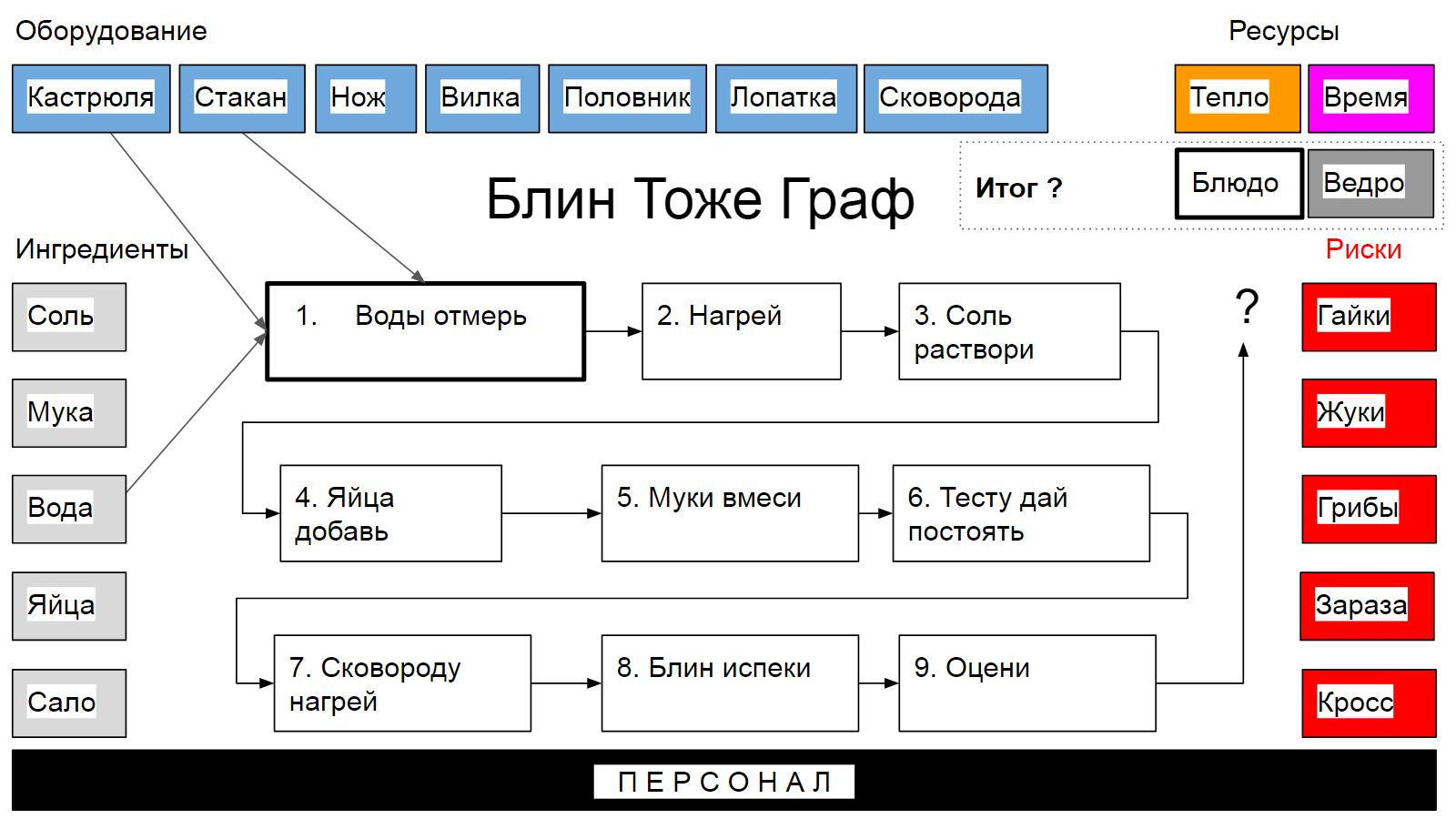
Далее, растворим рассоле яйца. Добавим муки и доведём тесто до необходимой консистенции. Дадим тесту постоять. Нагреем сковороду. Смажем кусочком сала, нанизанным на вилку. Блин испечём. И будем решать задачу бинарной классификации и искать ответ на вопрос - куда блин отправлять. На блюдо или в ведро?

Обычно рецепт приготовления и сам процесс - укладывается в довольно строгие рамки, отклонения от которых приведут к тому, что в результате стряпни будут получаться не блины, а комочки или что ещё похуже. Контроль формы графа, отражающего процесс приготовления отдельного блина и сравнение её с эталоном позволяет принять решение о выходном контроле “не глядя”. Такой подход называется Quality by Process - если все шаги были выполнены верно, то и блин вышел. Ещё одна задача системы контроля качества - разбор полётов. Ну ушёл блин в корзину, ну и что такого? Один, другой, третий. Похоже, что-то в системе не так. В этом случае нас интересует, в какой части граф отличается от эталонного.

Кроме отклонений от истинного пути, на кухне блину грозят риски: болты и гайки или просто мусор может попасть в муку, для борьбы с этим мы используем сито и проверенных поставщиков, гарантирующих качественные ингредиенты. Кроме того, есть всякие насекомые-вредители, которых хорошо бы не пускать на кухню. И плесень всякая. Чистота - залог здоровья. Кроме того, есть ещё бактерии, с которыми справится температурная обработка. А также - риск перекрёстного заражения (это когда одну доску используют для резки мяса и овощей в салат - образованные поварята за такое не только по рукам бьют).

В общем, когда вы опишете весь процесс производства по шагам, для каждого из них определите риски и меры по их предотвращению, а также ответственных по их воплощению, то у вас будет готова схема HACCP. И это позволит отправить пироженки в космос.

Итак, мы прошлись по основам теории графов - увлекательной области математики, позволяющей формально описать всё что угодно и заняться машинным обучением на этих данных. Для закрепления материала вам предстоит выполнить домашнее задание.

Использованные материалы и ссылки: