Knowledge Graph Embeddings

Материалы Ссылка
Видео YouTube
Слайды pdf
Конспект здесь
Домашнее задание link , colab

Видео

Векторные представления графов знаний

В первой части курса мы рассматривали символьные представлениях графов знаний (knowledge graph, KG) на основе стандартов RDF и OWL. И теперь мы знаем, как с помощью этого стека организовывать хранение, обработку и базовый логический вывод.

Во второй части мы фокусируемся на векторных представлениях (embeddings, эмбеддинги) и на том, как решать новые задачи с помощью методов машинного обучения (machine learning, ML) и этих векторных представлений. На этот раз, каждой сущности (вершине) и предикату (типу ребра) ставится в соответствие уникальный вектор (эмбеддинг) в некотором пространстве.

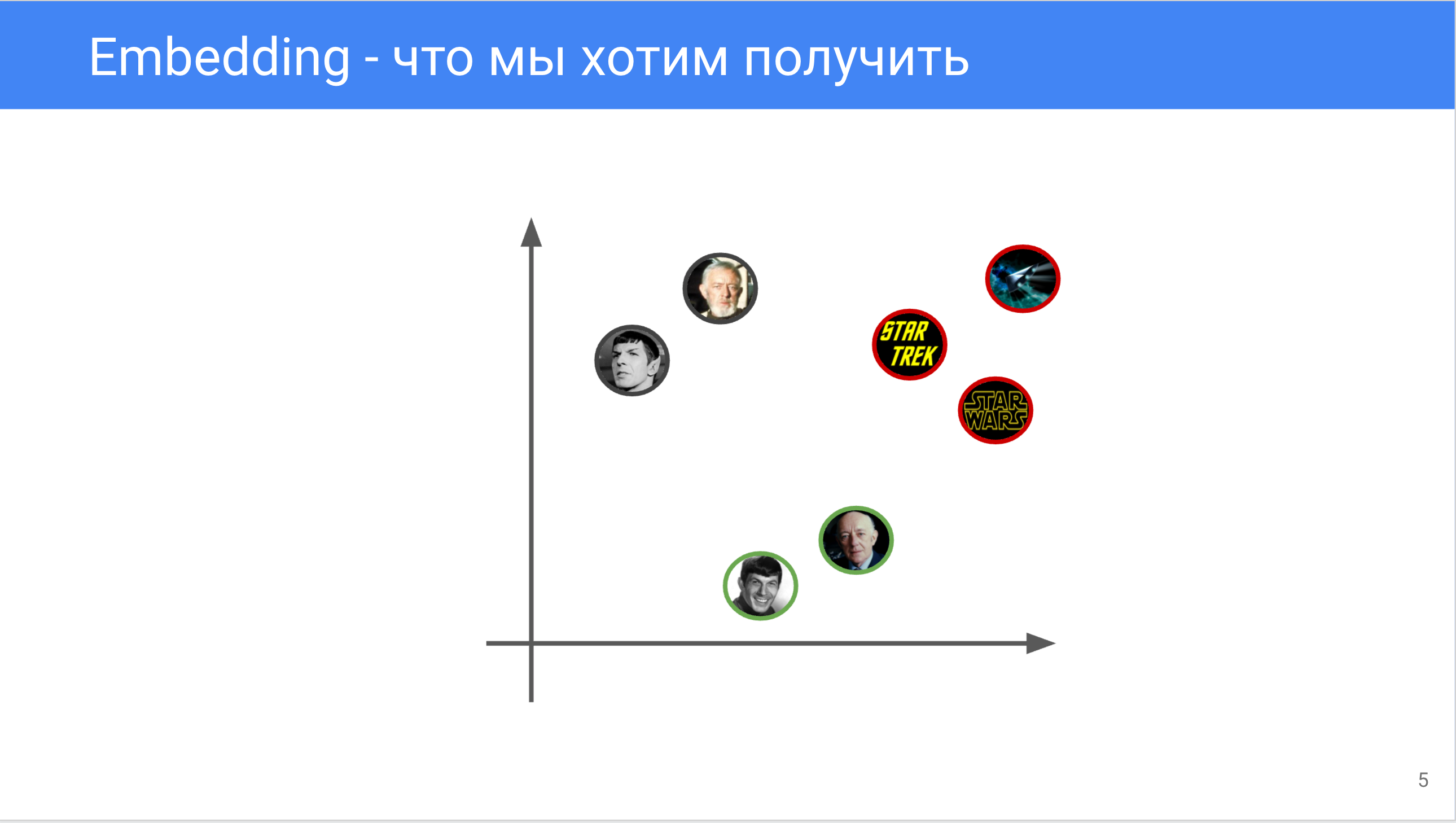
Setup

Количество задач над графами, которые можно решать с применением ML, весьма велико, и каждая из задач может подразделяться на отдельные проблемы в зависимости от условий (settings). Схематичное изображение актуальных проблем и условий изображено ниже:

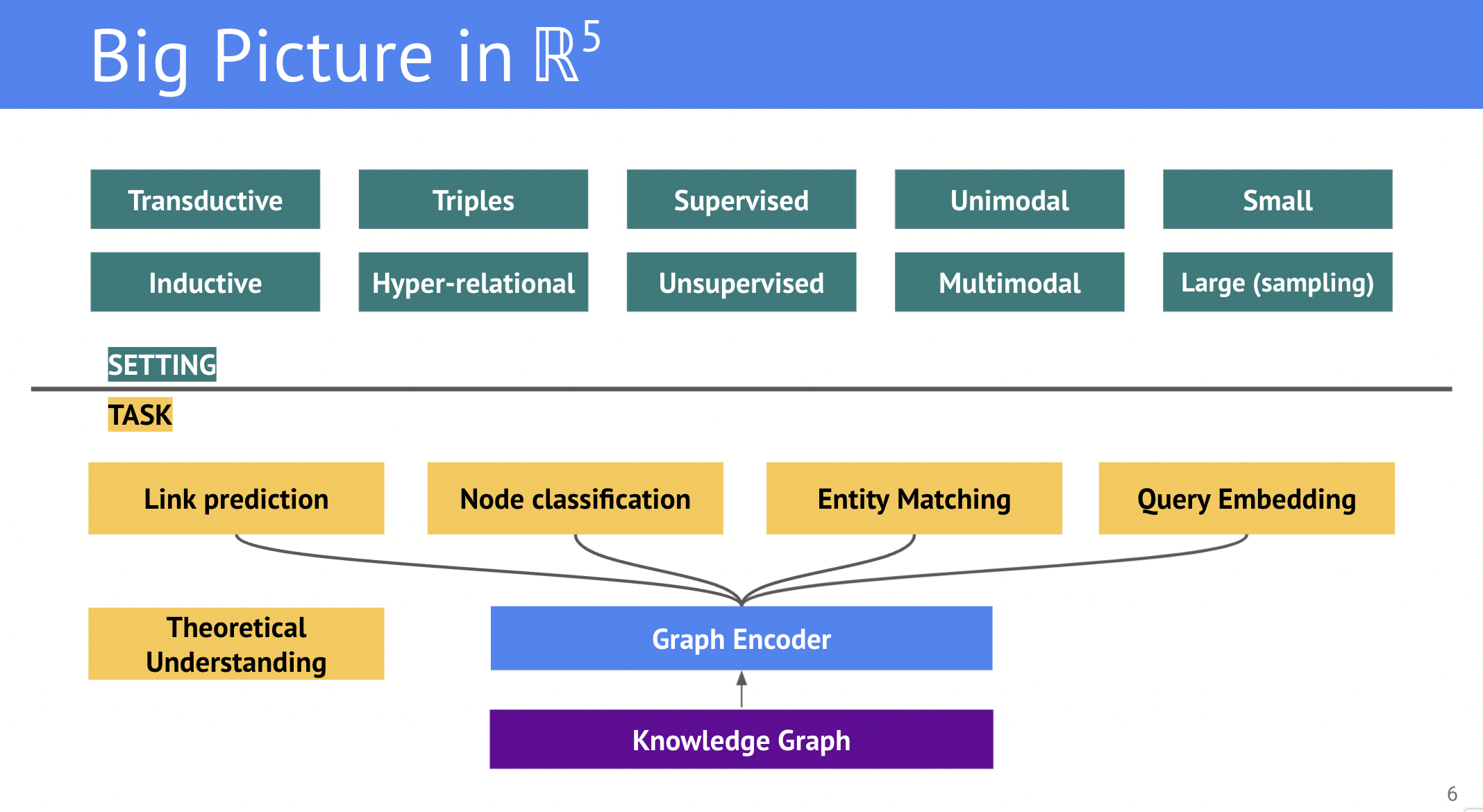
Для более простого введения в тему, в этой лекции рассматриваются способы построения векторных представлений для задачи предсказания связей (link prediction) в классических условиях:

  • Трансдуктивность (transductive) - все сущности и типы связей известны на момент тренировки, появление новых не допускается
  • Триплетные графы - целевые графы основаны только на триплетах (без сложных утверждений из RDF*), причем на только на объектных триплетах без литералов, чисел, дат, и прочих атрибутов
  • Обучение с учителем (supervised learning) - эмбеддинги оптимизируются напрямую через задачу link prediction, а сигнал - известные грани (связи) в графе.
  • Унимодальность (unimodal) - исследуемый граф состоит только из сущностей и предикатов, другие модальности (текст, видео, изображения) не допускаются
  • Малый размер - для простоты иллюстрации и заданий, рассматриваемые датасеты не содержат более 100 000 сущностей (узлов).

В предыдущей лекции были описаны базовые методы и алгоритмы машинного обучения на классических графах, под которыми мы будем понимать ненаправленные графы с одним типом ребра. Графы знаний (KG) отличаются от классических графов тем, что они:

  • Направленные
  • Мультиграфы (между двумя узлами может существовать больше одного ребра)
  • Типизированные ребра (каждое ребро имеет определенный тип из общего пула всех известных предикатов)

Более того, link prediction в классической формулировке определяет вероятность нахождения ребра между узлами $u$ и $v$ как функцию от двух узлов:

\[ p(link) = f(u, v) \]

В домене KG, такая формулировка соответствует задаче предсказания типа связи (relation prediction), тогда как link prediction (еще известен как knowledge graph completion, knowledge base completion) ставит задачу нахождения корретного объекта (субъекта) при заданном субъекте (объекте) и предикате: $(\textit{head},\textit{relation},?)$ или $(?, \textit{relation}, \textit{tail})$.

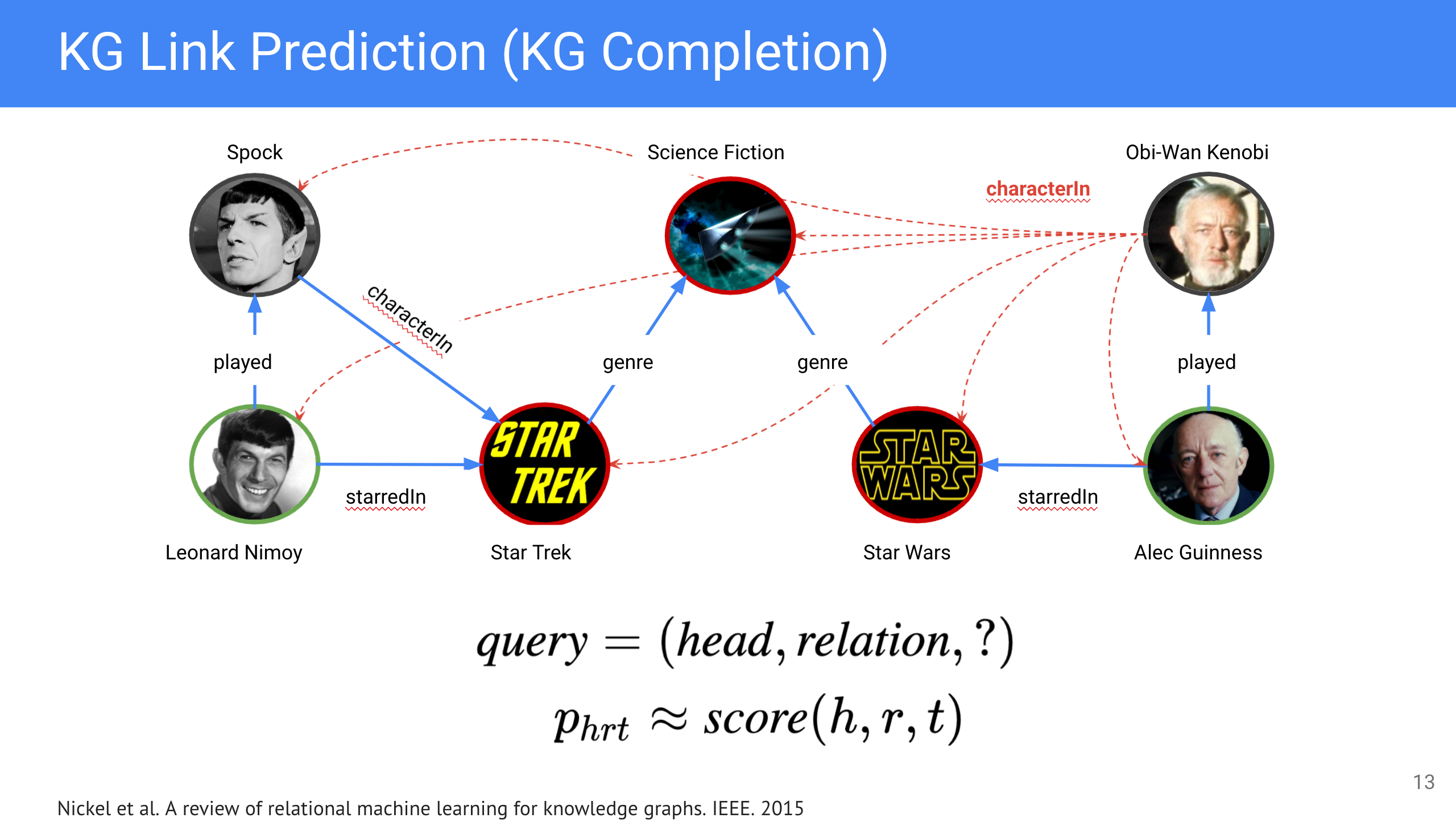Пример графа взят из оригинальной статьи [0]

Другими словами, мы подставляем на место предсказываемой сущности каждую известную сущность из KG и оцениваем степень корректности каждого такого триплета. Для этого, нам нужно иметь некоторую scoring function:

\[ p(h,r,t) \approx score(h, r,t) \]

Как правило, большинство алгоритмов KG embedding вводят свою собственную функцию оценки правдоподобности (scoring function).

Формат входных данных

Основная операция предобработки KG - замена всех URI сущностей и предикатов на числовые ID. Для этого создается два словаря (как правило, entity2id и relation2id), которые содержат маппинги URI на ID сущности или предиката. Способ нумерации может быть произвольный, но чаще ID назначаются после лексикографической сортировки URI.

Иллюстрируем на примере - пусть задан простой граф из трех вершин:

LeonardNimoy played Spock .
Spock characterIn StarTrek .
LeonardNimoy starredIn StarTrek .

Создав словари маппингов, на вход моделей будут подаваться закодированные триплеты

1 1 2
2 2 3
1 3 2

Созданные ID затем используются для указания соответствия строки эбмеддинг матрицы конкретной сущности или предикату.

Паттерны связей (Relational Patterns)

Выразительность (экспрессивность) эмбеддинг алгоритмов характеризуется возможностью моделировать паттерны, часто присутствующие в реальных KG:

  1. Симметричность: $r(h,t) = r(t,h)$ 
    knows(a, b) -> knows(b, a)
  2. Антисимметричность: $r(h,t) \ne r(t,h)$ 
    friend(a, b) -> ¬friend(b, a)
  3. Инверсия: $r_1(h,t) = r_2(t,h)$ 
    castMember(a, b) -> starredIn(b, a)
  4. Композиция: $r_1(h,t) \land r_2(t,z) \rightarrow r_3(h,z)$ 
    mother(a, b) ⋀ husband(b, c) -> father(a, c)
  5. Отношения: “один ко многим” $r(h,t_1),\dots,r(h,t_n)$ 
    hasCity(Russia, Moscow)
hasCity(Russia, Saint Petersburg)

    Отношения “один ко многим” часто встречаются в графах из-за наличия узлов-хабов, соединяющих большое число соседей.

Семейства KG Embedding алгоритмов

Основную задачу построения векторных представлений можно сформулировать следующим образом:

Близость представлений в векторном пространстве должна отражать семантическую близость вершин в исходном графе

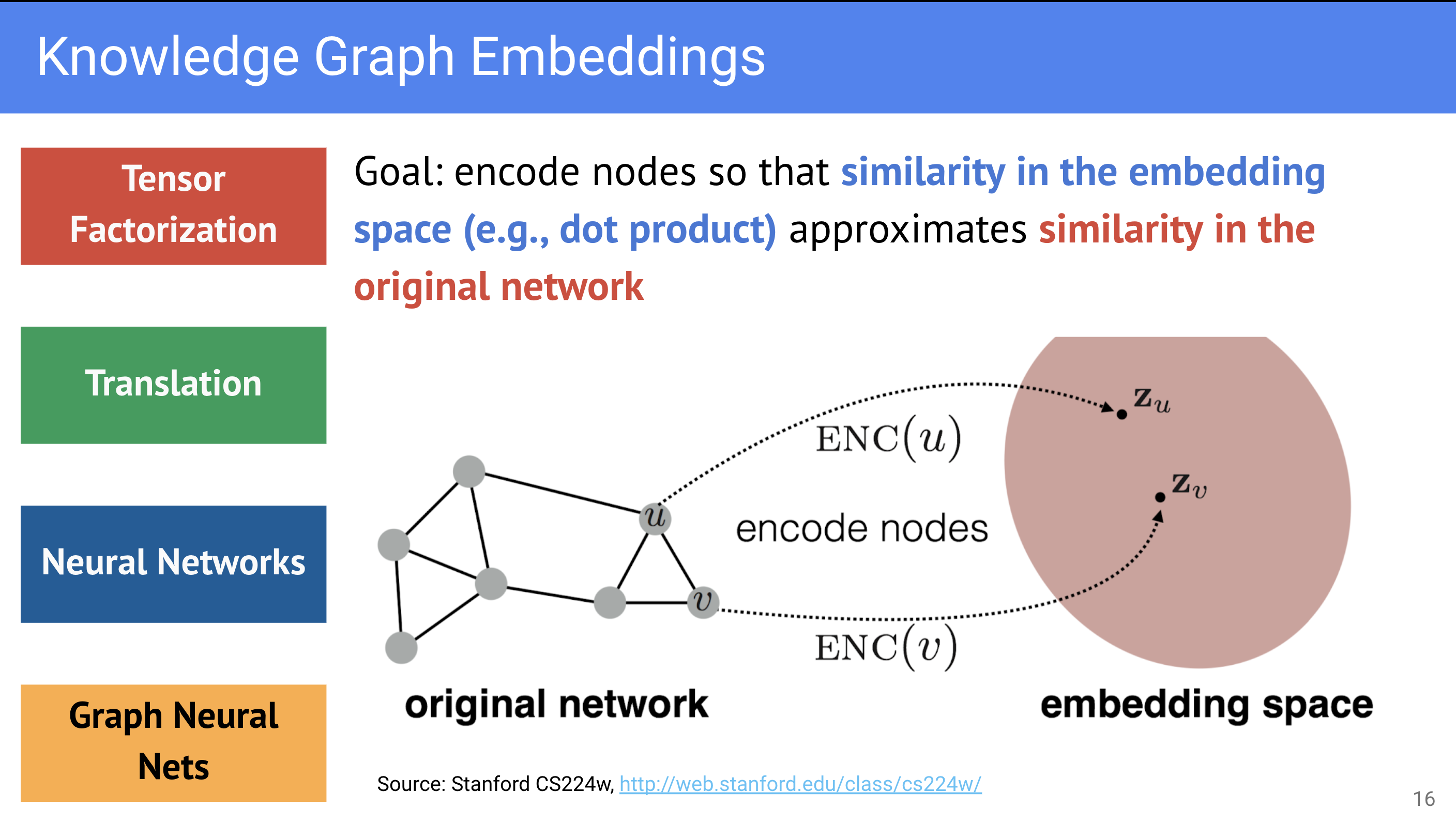
В этой лекции мы будем рассматривать shallow embedding модели, то есть алгоритмы, которые ставят каждой вершины и каждому предикату свой уникальный вектор (или матрицу).

Shallow алгоритмы можно классифицировать на три семейства:

  1. Алгоритмы, основанные на факторизации разреженного тензора смежности графа (Tensor Factorization)
  2. Трансляционные алгоритмы (Translation-based), моделирующие взаимодействия между сущностями как смещения (трансляции) их векторов
  3. Нейросетевые алгоритмы на популярных архитектурах (CNN, Transformer, и другие). Часто у них нет прямой геометрической интерпретации как у 1-2.

Tensor Factorization

Направленные multi-relational мультиграфы (KG в их числе), могут быть естественно представлены в виде трехмерного тензора $\mathcal{T} \in \mathbf{R}^{|E|\times |E|\times |R|}$, где $|E|$ - количество сущностей, $|R|$ - количество предикатов.

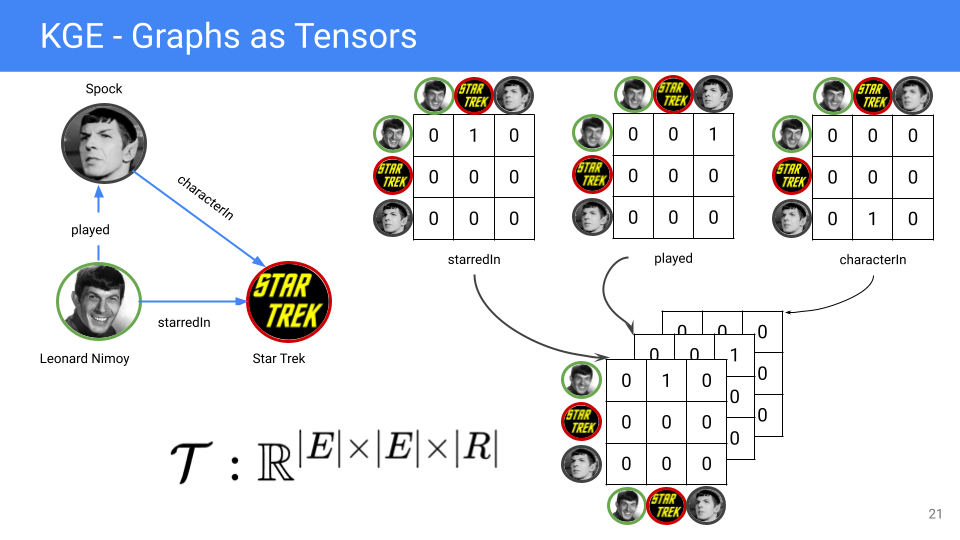
Рассматривая подграф, образованный каждым предикатом, мы можем составить его матрицу смежности (adjacency matrix) размером $|E|\times |E|$, где 1 - индикатор наличия триплета между сущностями в строке и столбце, 0 - отсутствие триплета. В силу направленности графа матрица смежности несимметричная. Объединяя $|R|$ матриц смежности (от каждого предиката), мы получаем тензор $\mathcal{T}$.

$\mathcal{T}$ - разреженный (sparse) тензор (число единиц намного меньше числа нулей), поэтому его неэффективно хранить в материализованном виде в памяти. Вместо этого, алгоритмы этого семейства делают неявную факторизацию (implicit factorization) это тензора с использованием триплетов (которые отвечают за число единиц в $\mathcal{T}$).

RESCAL

Ставший классическим, алгоритм RESCAL [1] напрямую факторизует разреженный $\mathcal{T}$ в плотные (dense) матрицы сущностей $E \in \mathbf{R}^{|E|\times d}$ и предикатов $W \in \mathbf{R}^{|R|\times d \times d}$

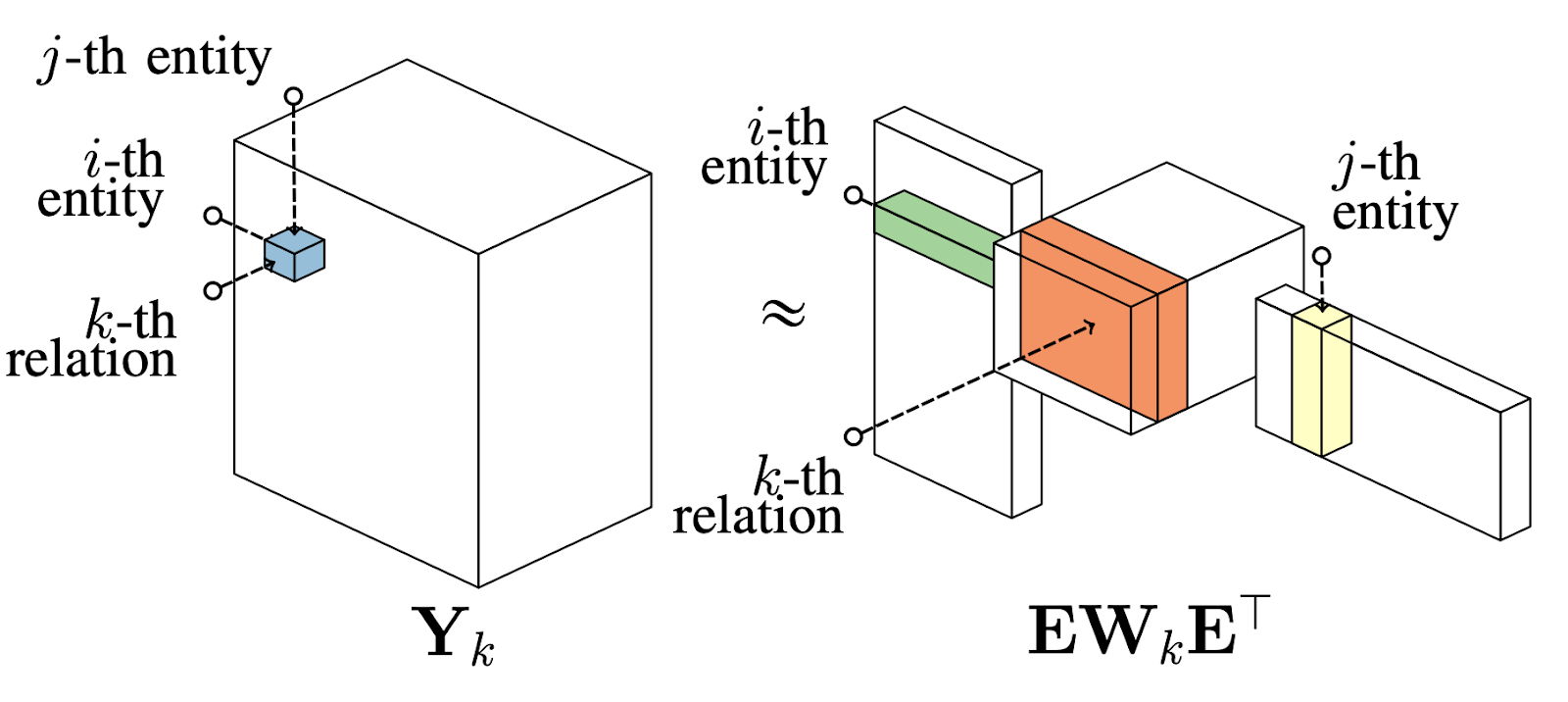Источник: оригинальная статья [1]

\[ \mathcal{T}_k = E \cdot W_k \cdot E^T \]

Тогда score function для триплета можно записать как:

\[ score(h,r,t) = h \cdot W_r \cdot t^T \]

Заметим, что RESCAL параметризует каждый предикат $r$ квадратной матрицей $W_r \in \mathbf{R}^{d\times d}$, из-за чего затраты на память растут квадратично в зависимости от размерности $d$ векторного пространства (и эмбеддингов), растет сложность тренировки и скорость переобучения модели.

DistMult

Проблему квадратных матриц решил DistMult [2], в котором предложили сделать матрицы $W_r$ диагональными (то есть с ненулевыми элементами только на главной диагонали), что позволило упростить score function:

\[ score(h,r,t) = \langle h,r,t \rangle = \| h \cdot r \cdot t \| \]

Теперь предикату соответствует вектор, а не целая квадратная матрица, и поэтому обе матрицы сущностей $E \in \mathbf{R}^{|E|\times d}$ и предикатов $R \in \mathbf{R}^{|R|\times d}$ растут линейно.

В силу коммутативности умножения, DistMult может моделировать симметричные предикаты $h \cdot r \cdot t = t \cdot r \cdot h$ и отношения “один ко многим” $h \cdot r \cdot t_1 \neq h \cdot r \cdot t_2$. По этой же причине DistMult не может моделировать антисимметричные и инверсные предикаты. Также не существует геометрической интерпретации паттерна композиции.

ComplEx

Умножение коммутативно в поле действительных чисел $\mathcal{R}$, но не комплексных $\mathcal{C}$. Авторы алгоритма ComplEx [3] и предложили использовать это свойство, переведя эмбеддинги сущностей и предикатов в комплексное пространство: $E \in \mathbf{С}^{|E|\times d}$, $R \in \mathbf{C}^{|R|\times d}$.

Каждое комплексное число $a+bi$ характеризуется парой действительных чисел $(a,b)$, поэтому на практике матрицы эмбеддингов сущностей и предикатов вдвое шире: $E \in \mathbf{R}^{|E|\times 2d}$, где первая половина считается действительной частью $Re(e)$ комплексного числа, а вторая - мнимой $Im(e)$.

 Score function использует действительную часть произведения трех комплексных чисел: субъекта $h$, предиката $r$, и комплексно сопряженного объекта $\bar{t}$:

\[ score(h,r,t) = \textit{Re}\langle h, r, \bar{t} \rangle \]

Такая операция некоммутативна, поэтому позволяет расширить поддерживаемые паттерны в дополнение к “один ко многим”:

  • Симметричные предикаты получаются, положив мнимую часть предиката равной нулю, $Im(r)=0$
  • Инверсные предикаты теперь являются комплексно сопряженными числами $r_1=\bar{r}_2$
  • Антисимметричность следует из свойств score function

Дальнейшие усовершенствования регуляризацией (ComplEx-N3 [4]) делают эту модель сильным baseline, с которым часто сравниваются новые публикуемые алгоритмы.

TuckER

Другой взгляд на факторизацию представляют авторы TuckER [5], предложившие рассматривать предыдущие способы факторизации как частные случаи декомпозиции Такера.

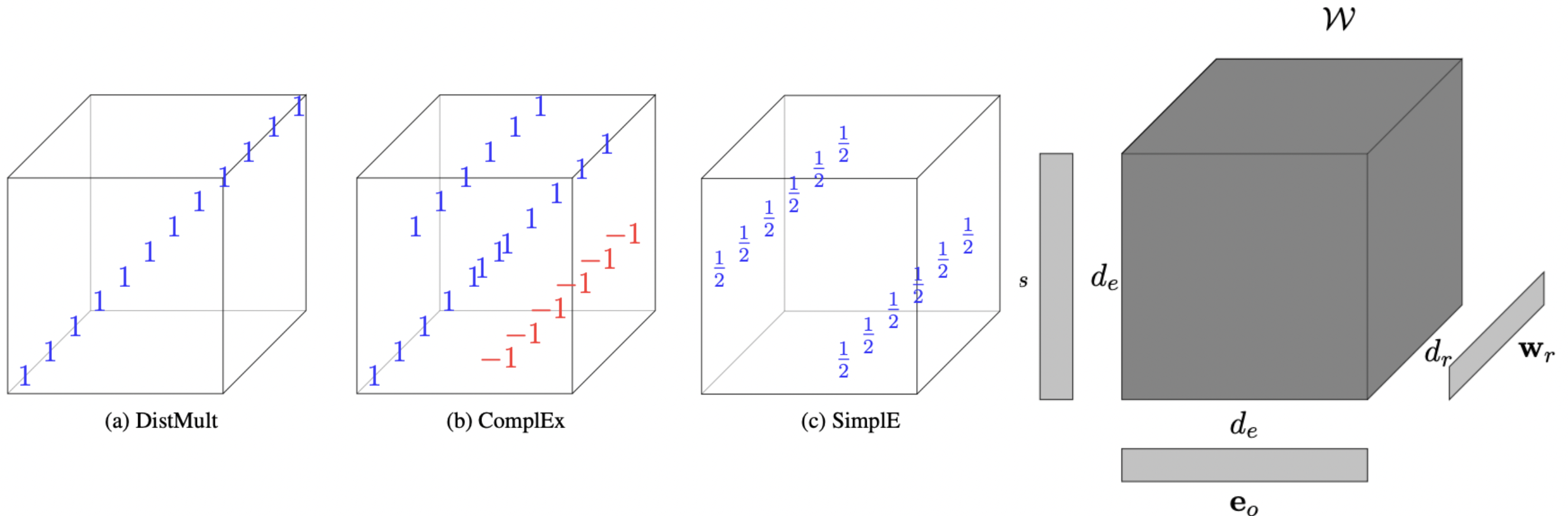Источник: оригинальная статья [5]

При этой декомпозиции в дополнение к матрицам $E \in \mathbf{R}^{|E|\times d}$ и $R \in \mathbf{R}^{|R|\times d}$ появляется core tensor $\mathcal{W} \in \mathbf{R}^{d_e \times d_r \times d_e}$, который должен моделировать дополнительные взаимодействия между сущностями и предикатами. Тогда score function можно представить как:

\[ score(h,r,t) = \mathcal{W} \times_1 h \times_2 r \times_3 t \]

где $\times_i$ описывает тензорное умножение по моде $i$.

Также авторы показывают, что DistMult, ComplEx и другие алгоритмы факторизации есть частный случай TuckER, налагающие определенные ограничения на содержимое core tensor $\mathcal{W}$.

Translation

Трансляционные (translation-based) алгоритмы имеют четкую геометрическую интерпретацию.

TransE

Классический алгоритм из этого семейства, TransE [6], моделирует взаимодействие субъекта (head) и предиката (relation) в виде векторной суммы их эмбеддингов. Таким образом, вектор объекта (tail) приблизительно равен сумме head и relation : $h + r \approx t$

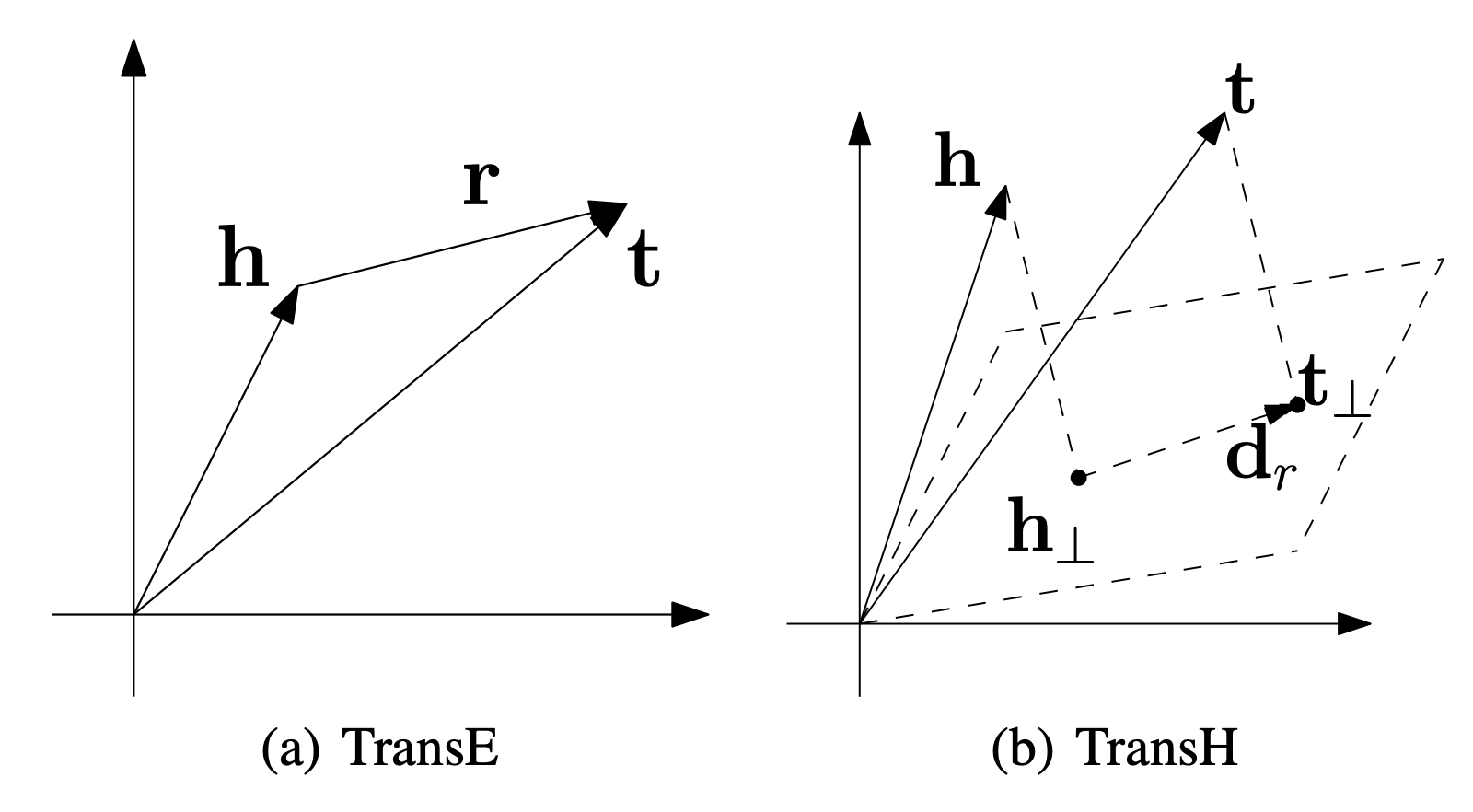Источник: [7]

TransE score function записывается весьма просто:

\[ score(h,r,t) = - \| h + r - t \| \]

Из этой функции следует, что TransE не может моделировать симметричные предикаты ($h+r -t \neq t+r-h$) и отношения “один ко многим”, так как при заданных $h+r$ все эмбеддинги объектов $t_1, \dots, t_n$ должны быть практически одинаковыми ($t_1 \approx t_2 \approx t_n$).

С другой стороны, TransE может моделировать антисимметричность, инверсные предикаты (положив $r_2 = -r_1$) с простым геометрическим смыслом (противоположно направленный вектор), а также композицию как сложение эмбеддингов предикатов: \[ h+r_1 \approx t_1 , t_1 + r_2 \approx z , \rightarrow h + (r_1 + r_2) \approx z \]

TransE положил начало семейству TransX алгоритмов, изменяющих исходную функцию тем или иным образом, например TransH [7] (на иллюстрации) дополнительно проецирует векторы сущностей в новое подпространство. Обзор этих методов можно найти в [9].

RotatE

Похожим образом, как ComplEx решил несколько проблем DistMult использованием комплексных числе, алгоритм RotatE [8] усовершенствует TransE, помещая эмбеддинги в комплексную плоскость и моделируя взаимодействие head и relation как вращение в этой комплексной плоскости. Тогда TransE является частным случаем RotatE, когда все мнимые компоненты равны нулю ($Im(e)=0$) и все взаимодействие происходит только в области действительных чисел (как на иллюстрации ниже).

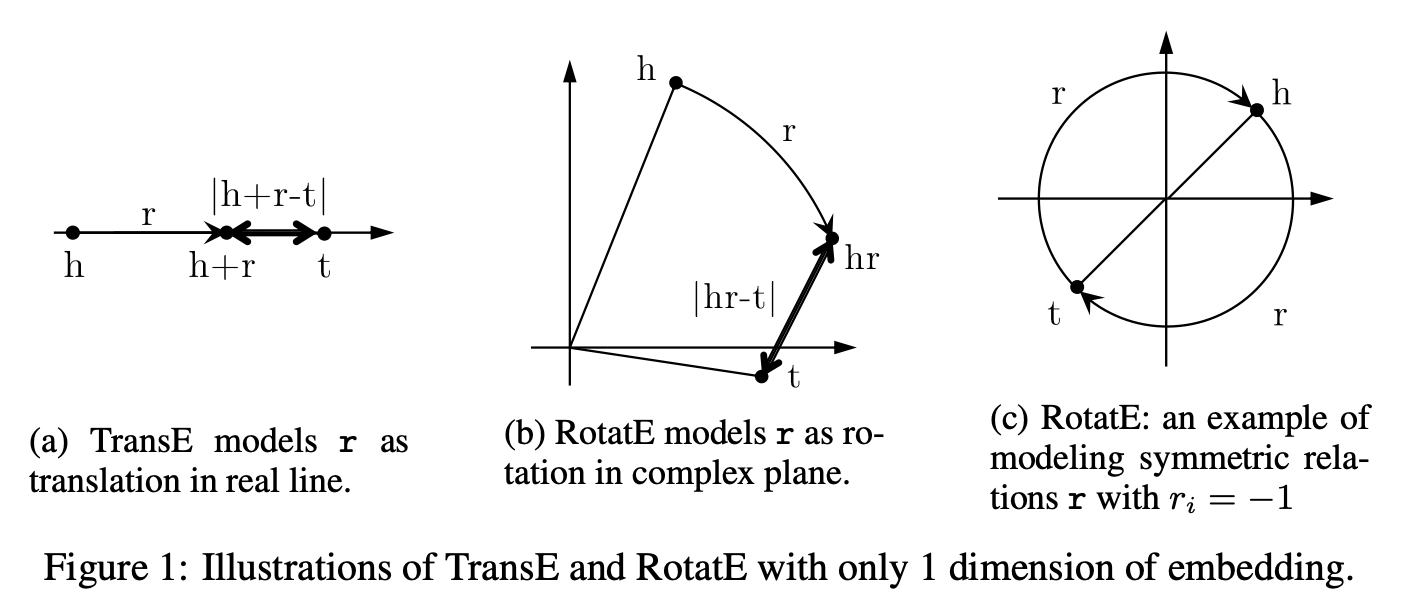Источник: [8]

Score function записывается следующим образом:

\[ score(h,r,t) = - \| h \circ r - t \| \]

С ограничением на модуль комплексного числа предиката $r$ : $|r|=1$.

RotatE теперь может моделировать симметричные предикаты, полагая вектор такого предиката как вращение на 180 градусов в комплексной плоскости.

Гиперболические модели

В последнее время стали активно развиваться подходы, делающие эмбеддинг в неевклидовы пространства, чаще всего - в гиперболические многообразия (hyperbolic manifolds), например, в n-размерный шар Пуанкаре (Poincare ball).

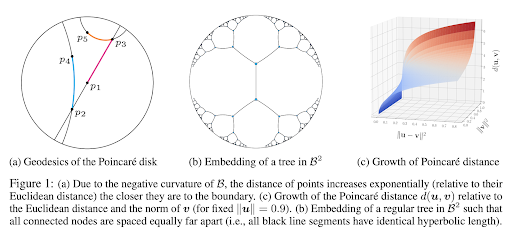Источник: [10]

В гиперболическом пространстве особенно хорошо моделириуются иерархические структуры - например, классовые иерархии и деревья. Корень иерархии будет находиться в центре шара, и все последующие уровни располагаются ближе к границе по экспоненциально убывающей дистанции. Хороший пример проекции иерархии в гиперболическое пространство - визуализация классовой иерархии из онтологии DBpedia:

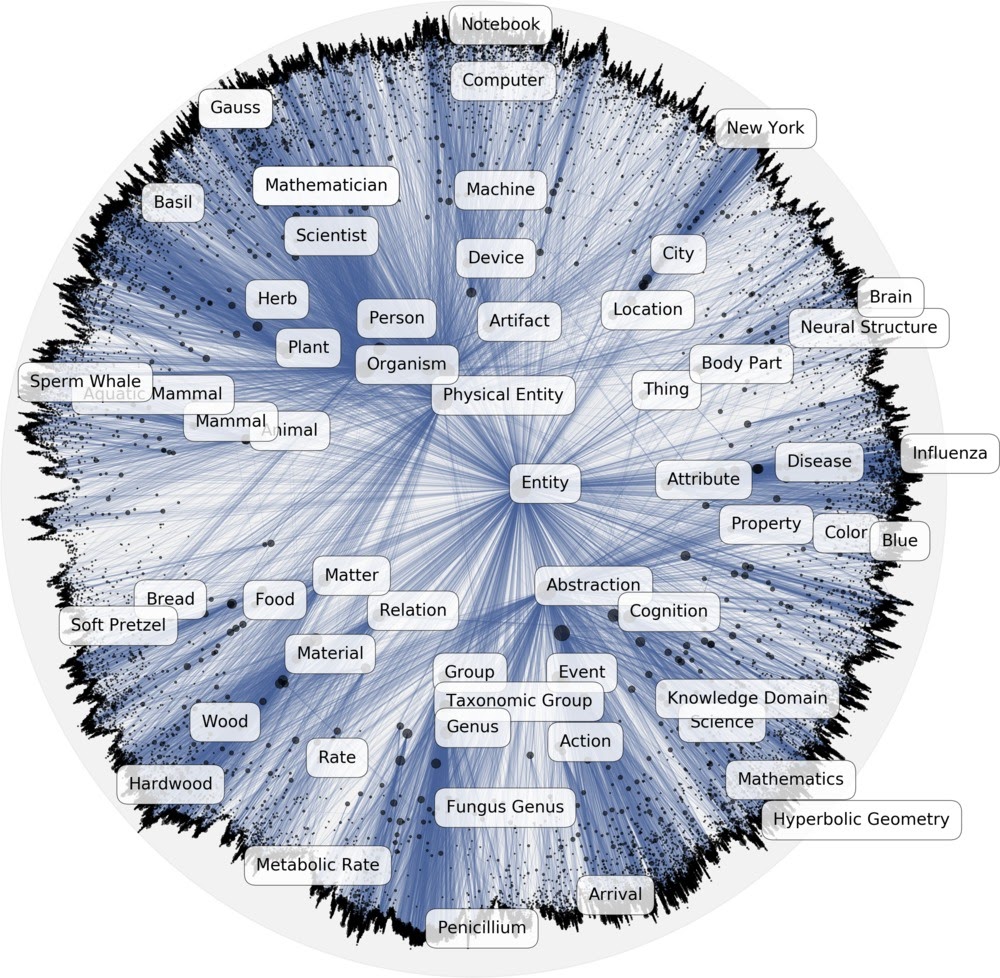Проекция онтологии DBpedia в гиперболическом пространстве. Источник: [10]

Гиперболические модели работают лучше евклидовых на малых размерностях векторов (32-64d) особенно на дерево-подобных графах как WordNet. Визуализация проекции обученных эмбеддингов действительно напоминает дерево-образную структуру:

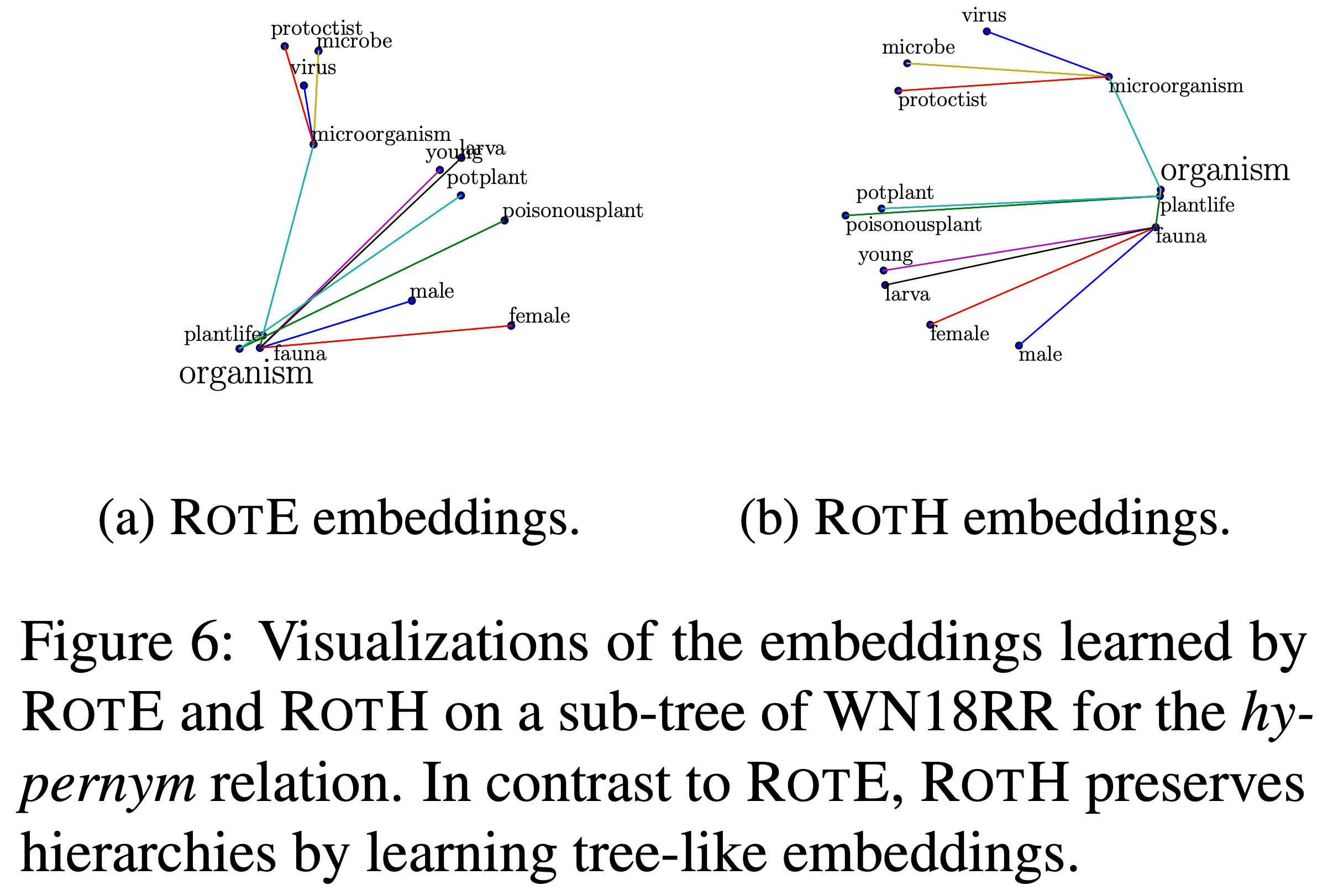Гиперболические эмбеддинги из WordNet. Источник: [11]

С другой стороны, гиперболические модели непросто обучать - нужны или оптимизаторы, способные работать с градиентом на многообразиях или работать в танценгиальной (локально-евклидовой) проекции.

Neural Networks

Нейросетевые подходы могут не иметь прямой геометрической интерпретации как предыдущие подходы, но в силу свойства универсальной аппроксимации такие подходы демонстрируют конкурентное качество на задаче link prediction.

CNN - ConvE

Простой способ применить конволюционные сети (CNN) предложили авторы ConvE [12]. Для этого, эмбеддинги head и relation группируются и трансформируются (reshape) в подобие 2D “изображения”. Получившийся тензор пропускается через конволюционные фильтры с полносвязным слоем в конце. Последним шагом считается dot product similarity эмбеддинга пары $f(h,r)$ и транспонированной матрицей всех сущностей $E$ как $f(h,r) \cdot E^T$. В результате получается распределение вероятностей по каждой сущности на предмет нахождения в позиции объекта триплета.

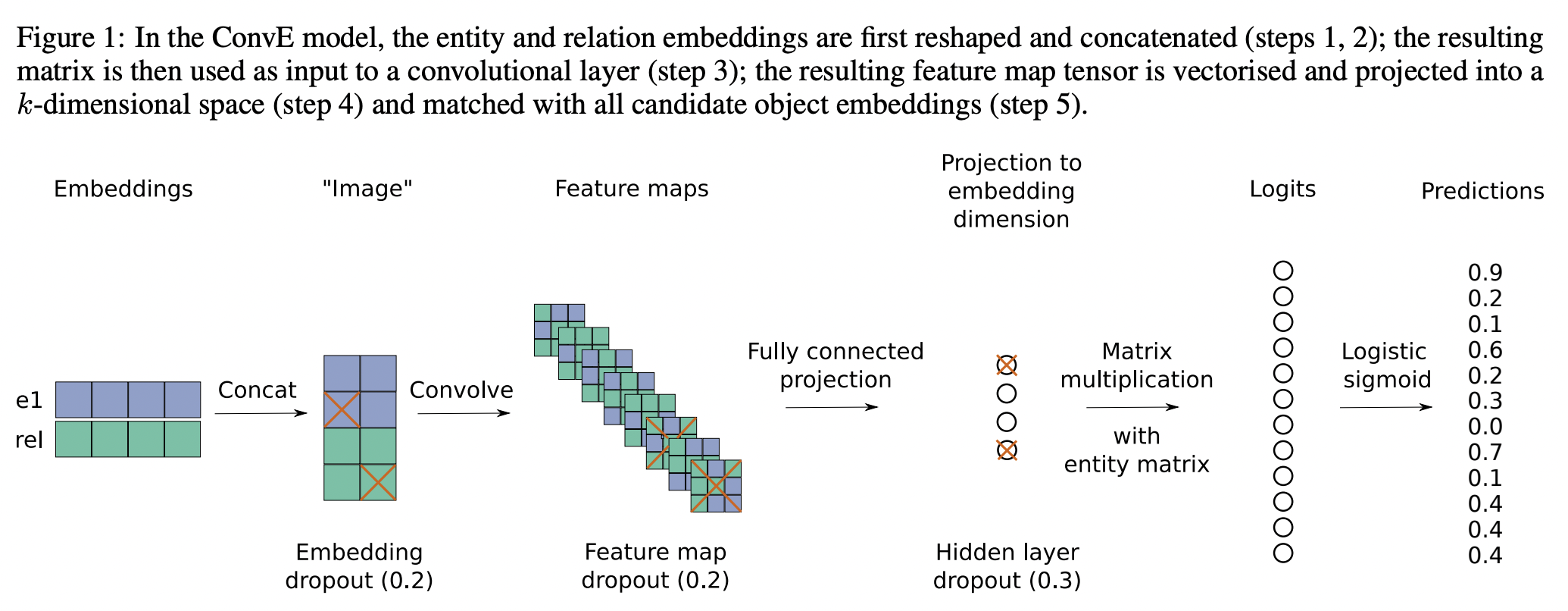ConvE. Источник: [12]

Так как модель тренируется предсказывать только объекты, задача предсказания субъекта $(?,r,t)$ переформулируется в предсказание объекта $(t,r^{-1},?)$ с добавлением инверсных триплетов (обозначаемых для простоты $r^{-1}$) в исходный граф (1-N scoring, о котором поговорим в следующей части лекции).

ConvE также породил большое число алгоритмов, использующих другие механизмы свертки или вводящих новые inductive biases, например ConvKB, ConvR, ConvTransE, etc.

Transformer - CoKE

Трансформеры [14] тоже могут служить энкодером над сгруппированными эмбеддингами сущностей и предикатов. Алгоритм CoKE [13] формулирует link prediction как задачу, похожую на языковое моделирование (language modeling) - по исходной последовательности токенов предсказать замаскированный (MASK) токен. В случае link prediction, этот замаскированный токен будет объектом триплета $(h,r,?)$ или пути в графе $(h,r_1, r_2, \dots, ?)$.

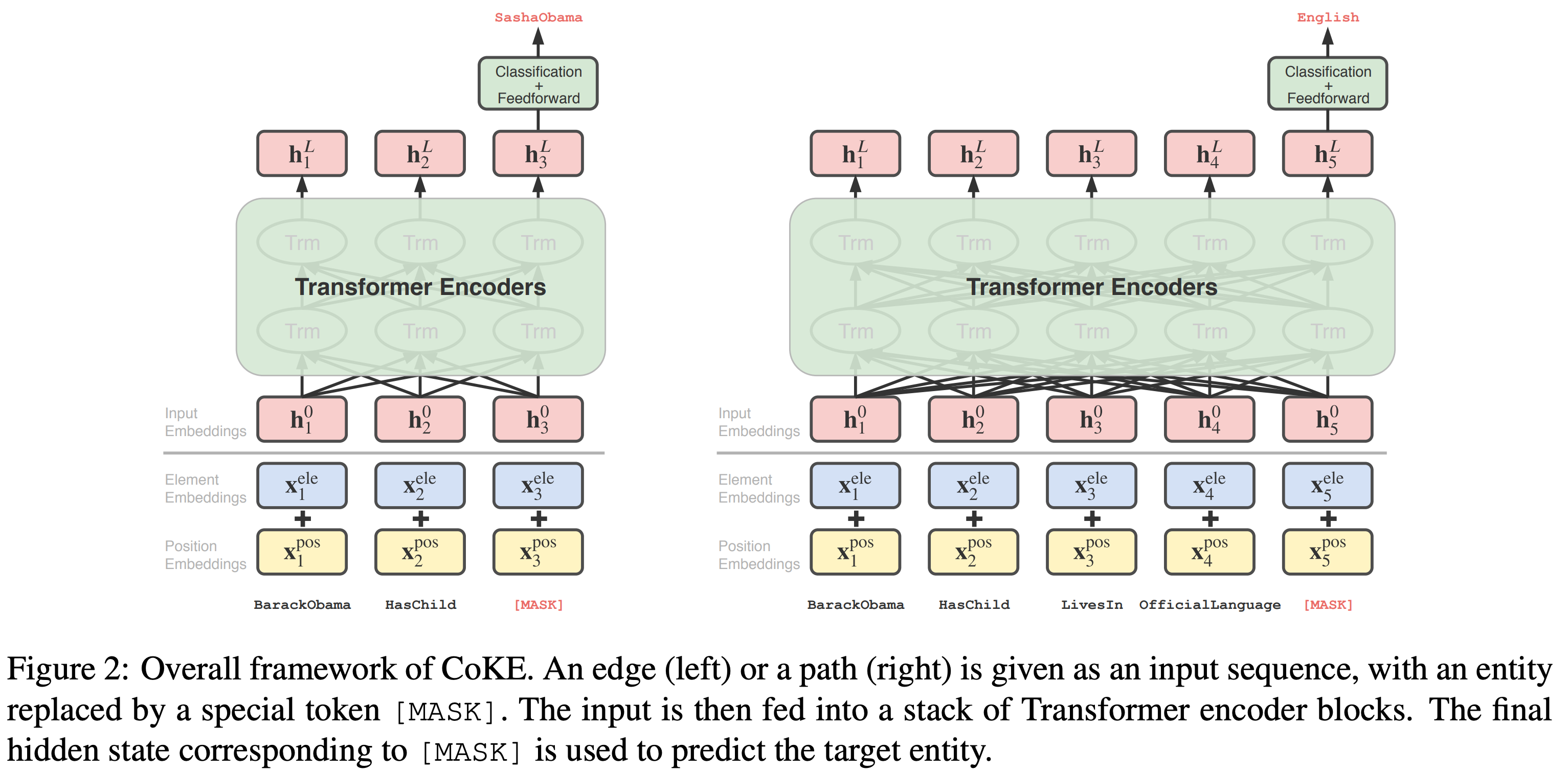Трансформер для link prediction в CoKE. Источник: [13]

Дополнительно обучаемые positional embeddings сообщают о позиции предиката в последовательности, а type emebddings вносят сигнал, позволяющий трансформеру отделить сущности от предикатов. Последним шагом, как в языковых моделях и в ConvE, эмбеддинг MASK токена умножается на транспонированную эмбеддинг матрицу сущностей $f_{MASK}(seq) \cdot E^T$.

Тренировка и функции потерь

Задача link prediction подразумевает ранжирование сущностей (объектов при $(h,r,?)$ или субъектов при $(?,r,t)$) от наиболее прадоподобных до наименее правдоподобных. Каждая эмбеддинг модель определяют свою score function правдоподобия, но процесс тренировки примерно одинаков. Напомним, что в трансдукивном варианте появление новых сущностей и предикатов не допускается, поэтому способ тренировки часто называют Local Closed World Assumption [15] (гипотеза локально-закрытого мира).

Разделяют два способа тренировки link prediction моделей:

  • Стохастический LCWA (stochastic LCWA, sLCWA) с использованием негативного семплирования (negative samplin) и контрастных функций потерь (contrastive losses), когда на каждый положительный триплет $(h,r,t)$ сэмплируется k некорректных примеров $(h,r,t’)$ (из k сущностей из общего множества $E$), и задача модели в том, чтобы функция правдоподобия оценивала корректный триплет выше всех некорректных, т.е. $score(h,r,t) > score(h,r,t’)$. Способ называется стохастическим, так как в качестве негативных примеров используется k случайных примеров, а не все $E$ сразу, и в результате тренировки случайные негативные примеры аппроксимируют функцию потерь от полного сравнения.
  • LCWA (1-N scoring), когда все триплеты сначала группируются по общим субьектам и предикатам (h,r): [t1, t2, ...] , и модели предсказывают распределение по всем сущностям, пытаясь повысить оценки для t1, t2, .. и занулить все остальные. В LCWA сценарии, как правило, необходимо добавлять инверсные предикаты $r^{-1}$, увеличивая количество триплетов и уникальных предикатов в два раза.

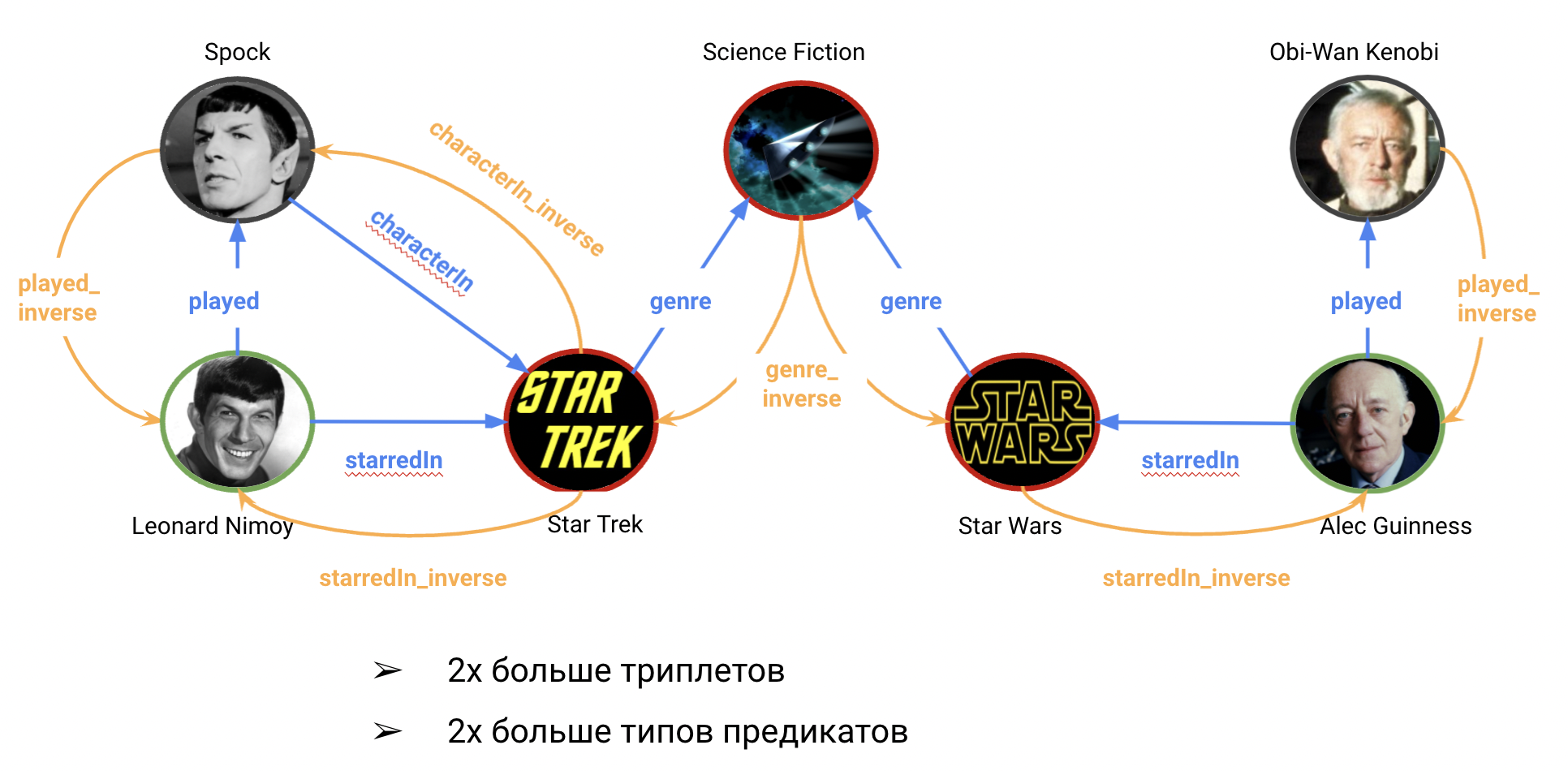Добавление инверсных предикатов и граней в исходный граф

Stochastic LCWA (sLCWA)

Стохастический LCWA (sLCWA) с применением негативного сэмплирования напоминает процесс тренировки классического word2vec. Для каждого триплета $(h,r,t)$ в исходном графе мы генерируем k триплетов со случайно измененным объектом (получая $(h,r,t’)$) или субъектом ($(h’,r,t)$). При тренировке мы инструктируем модель оценивать корректные триплеты $\mathcal{T}$ выше некорректных $\mathcal{T’}$ с учетом зазора (margin) $\gamma$.

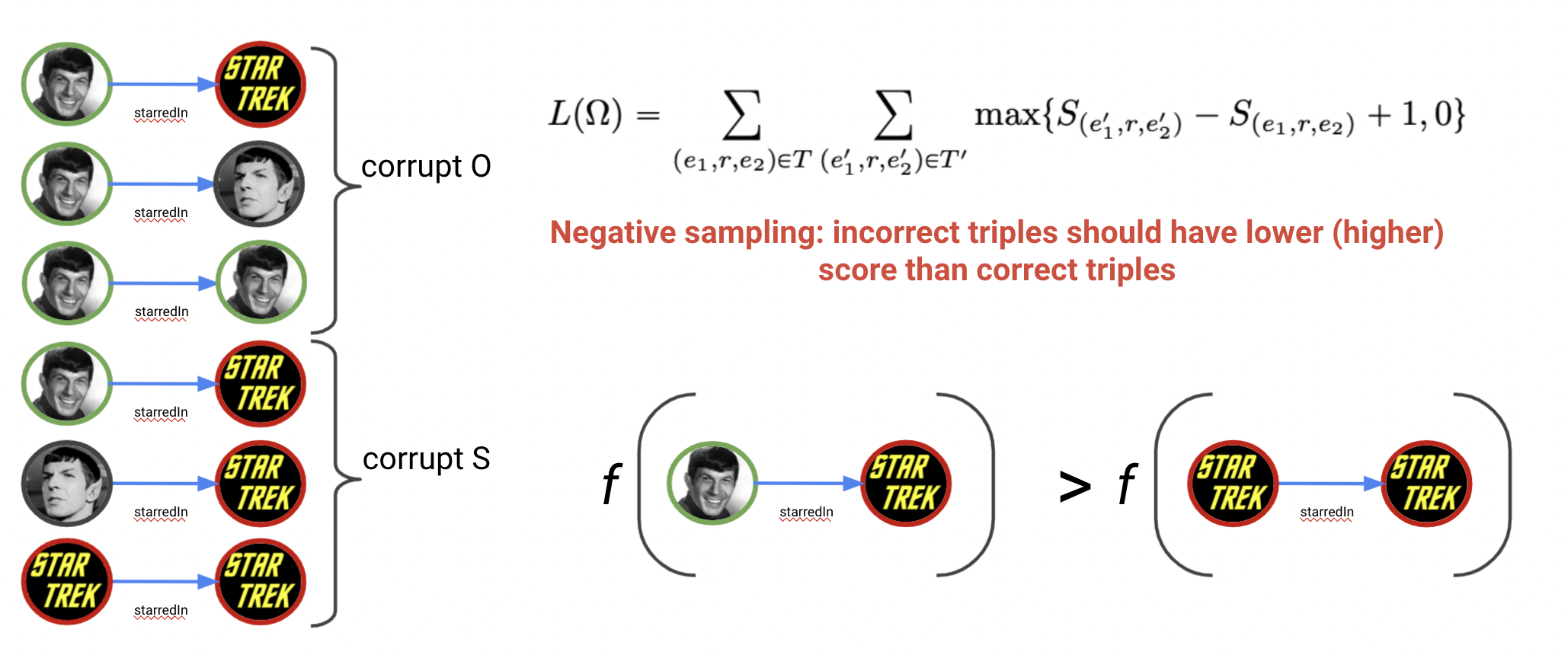Негативное сэмплирование - изменение head и tail сущностей

  • Из этого условия формулируется классический Margin Ranking Loss (MRL), с которым обучались в т.ч. TransE и DistMult:

\[ L = \displaystyle\sum_{(h,r,t) \in T } \displaystyle\sum_{(h,r,t’) \in T’} max \{ score(h,r,t’) - score(h,r,t) + \gamma, 0 \} \]

  • Авторы RotatE [8] усовершенствовали формулу, доподнительно взвешивая предсказания негативных триплетов через softmax с температурой $\alpha$, и создали Negative Sampling Self-Adversarial Loss (NSSAL):

\[ L = -\text{log} \sigma (\gamma - score(h,r,t)) - \displaystyle\sum_{i}^{k} p(h’_i,r,t’_i) \text{log} \sigma (score(h’_i,r,t’_i) - \gamma) \]

где

\[ p(h’_j,r,t’_j | \{ h’_i, r, t’_i \} ) = \frac{\text{exp} \, \alpha \, score(h’_j, r, t’_j)}{\sum_i \text{exp} \, \alpha \, score(h’_i, r, t’_i)} \]

  • Softplus (SPL) - способ применения классификационных функий потерь для негативного сэмплирования: \[ L(h,r,t,l) = \text{log} (1 + \text{exp} (-\hat{l} \cdot score(h,r,t))) \]

где метка $l$: $l \in \{ -1, +1 \}$, т.е. -1 в случае негативного триплета и +1 в случае корректного.

Характеристики sLCWA:

Плюсы Минусы
Output shape - $(bs * k, 1)$ Сходится медленнее
Низкие затраты GPU памяти Чувствительность к $\gamma$
Работает на больших графах Долгий evaluation

Гиперпараметр зазора $\gamma$ часто нужно подбирать для каждой модели для каждого датасета, т.к. даже малые колебания могут привести к большой разнице в качестве.

На валидации каждый триплет $(h,r,t)$ оценивается со всеми возможными комбинациями объектов $(h,r,t’)$ и субъектов $(h’,r,t)$. В стандартной формулировке sLCWA будет пропускать каждый из этих триплетов через модель, что очень долго по времени. Поэтому, как правило, даже при тренировке в sLCWA режиме с негативным семплированием оценку (на validation и test) делают в LCWA режиме 1-N.

Local Closed World Assumption (LCWA)

LCWA режим предполагает использование классифицикационных функций потерь, так как на выходе получается распределение вероятностей по всем известным сущностям в графе от заданной комбинации $(h,r)$, а не только по случайно выбранным $k$ триплетов как в случае негативного сэмплирования. Процесс обучения и оценки немного изменяется:

  1. Добавляются инверсные предикаты и инверсные грани в граф
  2. Триплеты графа во всех (train / validation / test) наборах группируются по общим субъектам и предикатам, образуя словарь (dictionary) вида (h,r): [t_1, ..., t_n]. Например, два триплета в исходном графе 
    Star Wars, cast member, Alec Guinness
Star Wars, cast member, Harrison Ford

    образуют один обучающий data point:

    (Star Wars, cast member): [Alec Guinness, Harrison Ford]
  3. Известные объекты пары $(h,r)$ с помощью one-hot encoding затем преобразуются в разреженный вектор меток размерности $[1,|E|]$, то есть создается распределение по всем сущностям графа, где 1 стоит на позиции известных объектов и 0 - во всех остальных случаях.

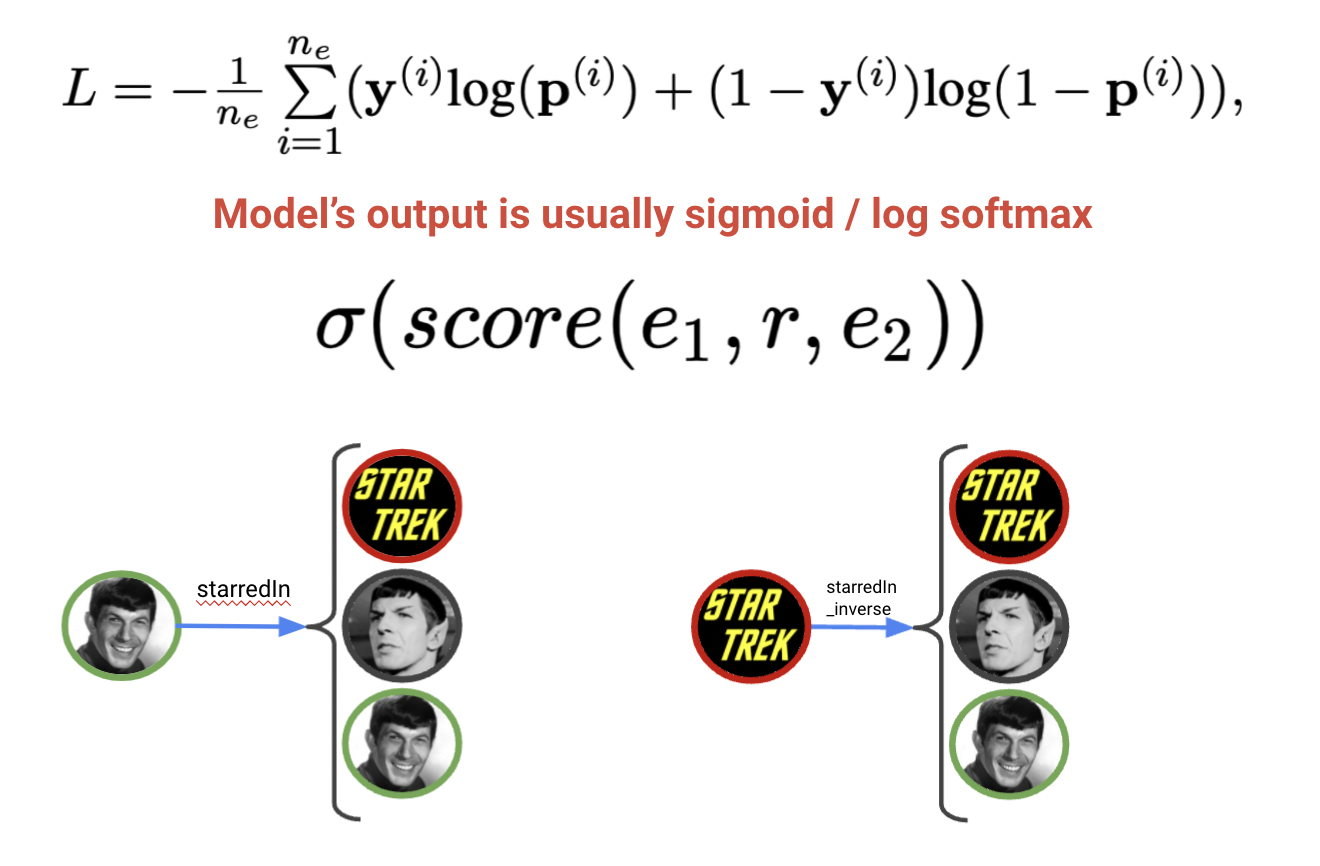1-N scoring

Таким образом, на вход LCWA моделей поступают пары $(h,r)$, и на последнем шаге любой модели эмбеддинг пары $f(h,r) \in \mathbf{R}^{1\times d}$, как правило, умножается на транспонированную матрицу всех сущностей $E^T \in \mathbf{R}^{d\times |E|}$ как dot product similarity. Получившееся распределение размерности $\mathbf{R}^{1\times |E|}$ подается в функцию потерь. Каждая сущность рассматривается как отдельный класс, поэтому используются классификационные функции потерь.

Применяемые функции потерь в LCWA:

  • Cross Entropy Loss (CEL) - где полученные score нормализуются через softmax, из-за чего CEL - multi-class single-label loss (то есть предполагает наличие единственной правильной метки).

\[ L = - \displaystyle\sum l(h,r,t) \cdot \text{log}(p(t | h,r)) \]

где $l(h,r,t)$ - бинарная метка, обозначающая корректность или некорректность рассматриваемого триплета.

  • Binary Cross Entropy Loss (BCEL) - где полученные score нормализуются через sigmoid независимо друг друга, делая задачу похожей на multi-class multi-label (то есть разрешает наличие нескольких правильных меток).

\[ L(h, r, t) = - \displaystyle\sum (l(h,r,t) \cdot \log(\sigma(f(h,r,t))) + (1 - l(h,r,t)) \cdot \log(1 - \sigma(f(h,r,t))) \] где $l(h,r,t)$ - бинарная метка, обозначающая корректность или некорректность рассматриваемого триплета.

Характеристики LCWA:

Плюсы Минусы
Сходится быстрее Output shape - $(bs, | E |)$
Нет доп. гиперпараметров Быстро растет потребление памяти GPU
Быстрый evaluation Софт-лимит в 100К сущностей

LCWA более требователен к GPU памяти, т.к. выходные shapes: $[bs, | E |]$, и тренировать графы со 100К и более сущностей становится сложнее и дороже.

Метрики оценки качества

KG link prediction - скорее задача ранжирования сущностей (вероятно являющихся объектом или субъектом), поэтому популярные метрики качества сходны с метриками из рекомендательных систем. Процесс оценки (на validation или test сетах) для каждого триплета $(h,r,t)$ состоит из трех шагов:

  1. Оценка предсказаний объекта $(h,r,?)$
  2. Оценка предскакзаний субъекта $(?,r,t)$
  3. Усреднение значений из шагов 1-2

Стоит заметить, что при добавлении инверсных предикатов (то есть всегда в LCWA режиме и опционально в sLCWA) шаг 2 выполняется как оценка предсказания объекта инвертированного триплета $(t,r^{-1}, ?)$. Собственно, для этого и необходимо обучение инверсных предикатов $r^{-1}$.

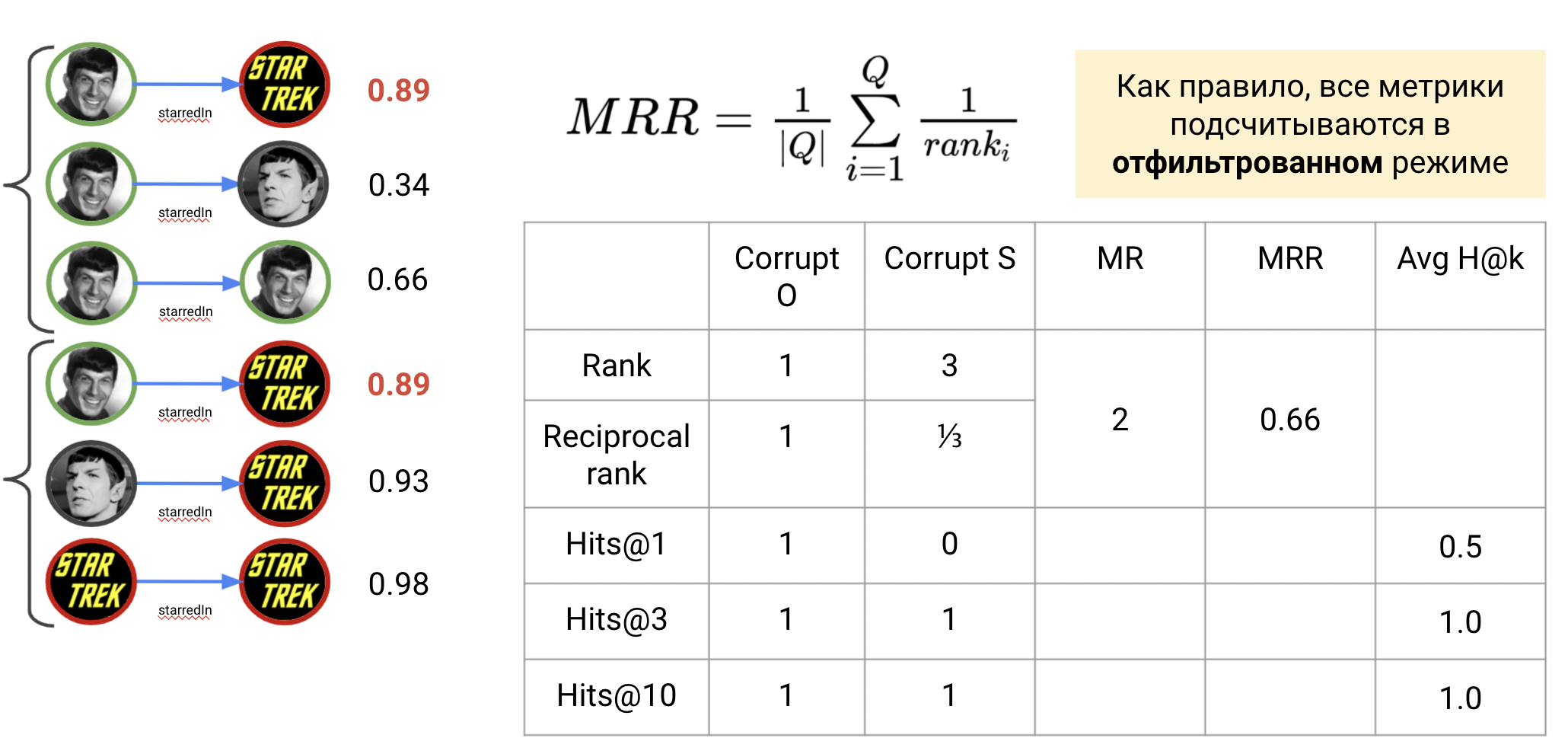Ранжирование и подсчет метрик

Mean Reciprocal Rank

На этапе оценки предсказаний для триплета $(h,r,t)$ модели строят распределения правдоподобности для каждой сущности, оторые могут быть значением score function напрямую или нормализованным значением (через sigmoid или softmax), отражающим вероятность. Затем сущности сортирутся по убыванию правдоподобности. Рангом искомой сущности $rank(t)$ (или $rank(h)$) называется позиция этой сущности в отсортированном списке (начиная с 1). Агрегацию по значениям рангов используют реже в силу подверженности этих значений выбросам, то есть несколько очень низких рангов способны значительно изменить агрегированное значение в худшую сторону. Вместо этого используют реципрокные ранги. Реципрокный ранк (reciprocal rank, RR) $rrank(t) = \frac{1}{rank(t)}$ считается как обратное значение ранга.

Тогда средний реципрокный ранг (mean reciprocal rank, MRR) - среднее значение реципрокных рангов для всех предсказаний оцениваемого блока (на шаге 1 или шаге 2). Принятно считать, что чем ближе MRR к единице, тем лучше качество модели.

\[ MRR = \frac{1}{|Q|} \displaystyle\sum_{i}^{Q} \frac{1}{rank_i} \]

На иллюстрации выше, на шаге 1 MRR равен 1, на шаге 2 равен 0.33, и агрегированное значение MRR 0.66.

Hits@K

Более точная метрика Hits@k показывает, попадает ли ранг искомой сущности в топ-k отранжированных предсказаний. Значение k, как правило, выбирается как $[1,3,5,10]$, то есть Hits@1 показывает, как часто модель предсказывает целевую сущность сразу на первом месте, а Hits@10 - в пределах первых 10 лучших предсказаний. Учитывая, что мы имеем дело с графами на десятки тысяч сущностей, Hits@k при малых k - довольно показательная метрика. Разумеется, если Hits@1 для триплета равен 1, то и все остальные Hits@k тоже равны 1. Принятно считать, что чем ближе Hits@k к единице, тем лучше качество модели. Однако, часто смотрят и на конкретный k - в некоторых задачах (например, information retrieval) более широкий диапазон Hits@10 важнее, а в других - важны более точные метрики Hits@1 или Hits@3.

На иллюстрации выше, на шаге 1 предсказание целевой сущности находится на первом месте, значит Hits@1 и все остальные Hits@k равны 1. Тогда как на шаге 2 ранг целевой сущности равен 3, значит Hits@1 равен 0, а Hits@3 и ниже равны единице. На шаге 3 все метрики усредняются.

Фильтрация

В реальных графах часто встречаются паттерны “один ко многим”, “многие к одному”, “многие ко многим” (например, из-за наличия hub nodes), и поэтому у оцениваемого триплета $(h,r,t)$ (и, соответственно, запроса $(h,r,?)$) может быть несколько корректных ответов $t_2, \dots, t_n$ помимо собственно $t$. Это важно учитывать при подсчете метрик, так как прочие корректные ответы могут быть отранжированы выше целевого и искусственно понизить качество предсказаний:

Фильтрация корректных, но нецелевых сущностей

В этом примере, оцениваемый триплет (Science Fiction, exampleMovie, Star Wars) имеет объект Star Wars, тогда как на запрос $(h,r,?)$ корректным ответом также будет Star Trek. Модель отранжировала Star Trek выше целевого Star Wars и ранг Star Wars, соответственно, стал равен 2, хотя, технически, модель не ошиблась.

Чтобы избежать подобных ситуаций, используют фильтрацию (filtered setting), когда предсказания прочих корректных сущностей для $(h,r,?)$ устанавливаются в низкое значение (как правило в $-inf$), чтобы при сортировке они оказались в конце списка и не влияли на подсчет метрик. В целом, значения метрик в отфильтрованном режиме должны быть выше, чем в нефильтрованном.

Подавляющее большинство современных KG embedding алгоритмов оценивается в фильтрованном режиме.

Больше метрик

Однако, даже после фильтрации модели могут назначать большому количеству объектов абсолютно одинаковые вероятности [16]. Тогда сортировка по убыванию будет возвращать недетерминированные результаты (одинаковые значения могут быть расставлены в случайном порядке). В зависимости от того, на каком месте при таком ранжировании находится целевая сущность, оценка может быть слишком оптимистичной (optimistic rank, всегда на первом месте среди равных) или пессимистичной (pessimistic rank, всегда на последнем месте среди равных). В таких случаях считают реалистичный сценарий (realistic rank) как мат. ожидание от оптимистичной и пессимистичной оценок.

Так, было обнаружено [17], что многие опубликованные модели докладывали только неестественно высокие оптимистичные оценки, которые при реалистичной оценке оказывались на уровне или хуже большинства известных моделей.

Более того, появляется больше новых метрик [16] (Adjusted Mean Rank, Geometric Mean Rank, etc), призванных более выпукло оценивать производительность моделей на разных уровнях в разных настройках.

Датасеты и бенчмарки

Исторически, основными бенчмарками для оценки качества KG link prediction стали графы на основе Freebase и WordNet. В старых оригинальных датасетах было обнаружно множество проблем - test set leakages и простые шаблоны, при которых системы на простейших правилах способны полностью решить задачу предсказания связей.

Старые, неиспользуемые датасеты (не используйте их):

  • FB15k
  • WN18

В дальнейшнем, эти датасеты были очищены в FB15k-237 и WN18RR, соответственно, и стали стандартными бенчмарками для оценки эмбеддинг моделей. Несмотря на улучшения, эти датасеты могут не донца отражать реальные графы, т.к. Freebase закрыт с 2014 года и с тех пор недоступен, а WordNet - слишком разреженный граф, похожий на дерево иерархий. Поэтому в последнее время стало появляться больше датасетов, основанных на Wikidata и других KG.

Таблица с базовой статистикой часто используемых датасетов:

  FB15k-237 WN18RR CoDEx YAGO 3-10 OGB WikiKG 2 KDD Cup Wikidata
# nodes 15k 40k 2-70k 123k 2.5M 87M
# edges 272k 80k 33-550k 1M 13M 504M
# predicates 237 11 42-69 34 1000 1,315

Подбор гиперпараметров по-прежнему очень важен, и несколько последних работ [15] [18] показали, что даже классические модели TransE, RESCAL и DistMult могут демонстировать высокую, сравнимую с современным state of the art, производительность на разных графах.

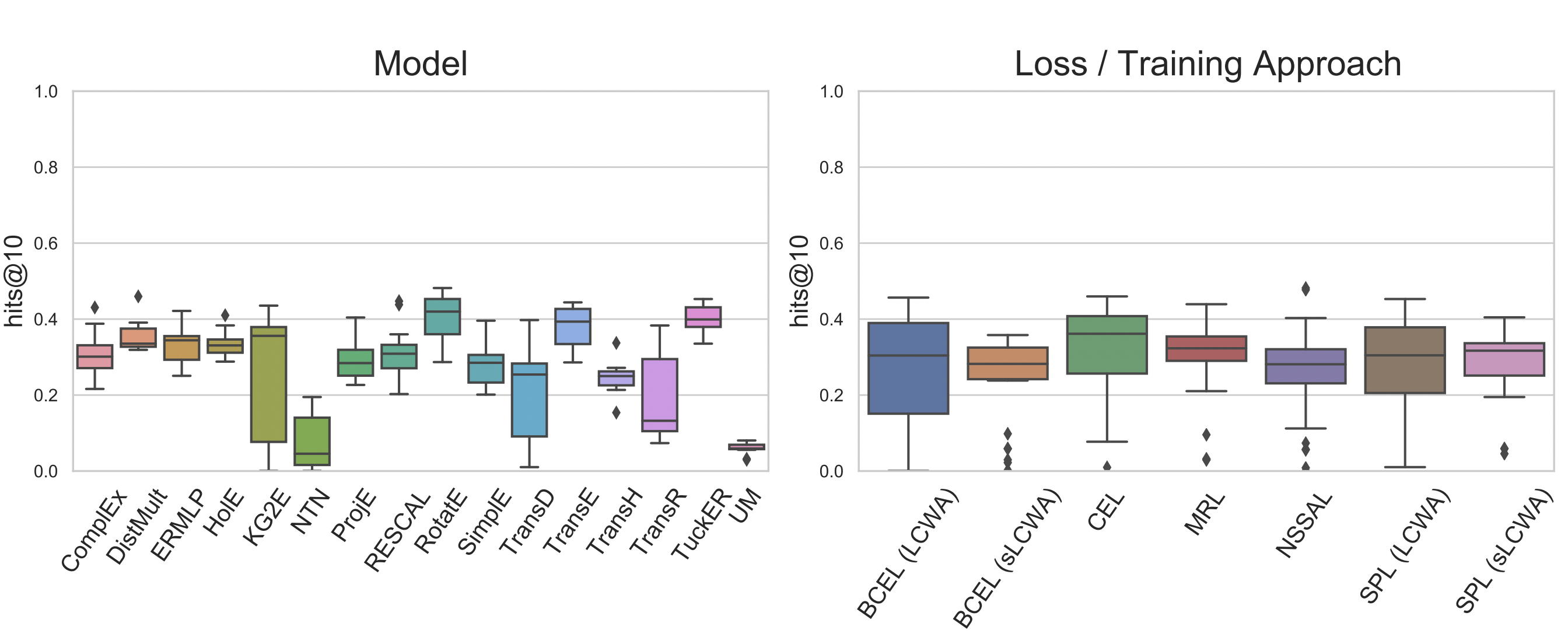Hits@10 популярных моделей на FB15k-237 после поиска оптимальных гиперпараметров. Источник: [15]

Библиотеки и репозитории

В практической части мы будем использовать библиотеку PyKEEN, где содержатся большинство описанных моделей, способов тренировки, оптимизации, и других компонентов.

Популярные библиотеки для работы с KG embedding:

Домашнее задание

  1. Выведите формулу ComplEx $\text{Re}\langle h, r, \bar{t} \rangle $ через конкретные действительные и мнимые части сущностей и предикатов как результат умножения трех комплексных чисел. Пусть каждое комплексное число $x$ состоит из $x_{re} + i \cdot x_{im}$.
  2. Выведите формулу Hadamard product между комплексными сущностью и предикатом RotatE $ h \circ r $. Представьте $r$ как через матрицу вращения, где $\text{cos}(r)$ можно положить за $r_{re}$ и $\text{sin}(r)$ как $r_{im}$. Эта матрица вращает $h$ - вектор-столбец из действительной и мнимой частей.
  3. Colab Notebook с набором заданий и примеров работы с KG embedding алгоритмами с библиотекой PyKEEN.

Использованные материалы и ссылки:

[0] Nickel, M., Murphy, K., Tresp, V. and Gabrilovich, E., 2015. A review of relational machine learning for knowledge graphs. Proceedings of the IEEE, 104(1), pp.11-33.
[1] Maximilian Nickel, Volker Tresp, Hans-Peter-Kriegel, “A Three-Way Model for Collective Learning on Multi-Relational Data”, Proceedings of the 28th International Conference on Machine Learning (ICML’11), 809–816, ACM, Bellevue, WA, USA, 2011
[2] Yang, Bishan, Wen-tau Yih, Xiaodong He, Jianfeng Gao, and Li Deng. “Embedding entities and relations for learning and inference in knowledge bases.” ICLR 2015.
[3] Trouillon, Théo, Johannes Welbl, Sebastian Riedel, Éric Gaussier, and Guillaume Bouchard. “Complex embeddings for simple link prediction.” In International Conference on Machine Learning, pp. 2071-2080. PMLR, 2016.
[4] Lacroix, Timothée, Nicolas Usunier, and Guillaume Obozinski. “Canonical tensor decomposition for knowledge base completion.” In International Conference on Machine Learning, pp. 2863-2872. PMLR, 2018.
[5] Balazevic, Ivana, Carl Allen, and Timothy Hospedales. “TuckER: Tensor Factorization for Knowledge Graph Completion.” In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 5188-5197. 2019.
[6] Bordes, Antoine, Nicolas Usunier, Alberto Garcia-Duran, Jason Weston, and Oksana Yakhnenko. “Translating embeddings for modeling multi-relational data.” In Neural Information Processing Systems (NIPS), pp. 1-9. 2013.
[7] Wang, Zhen, Jianwen Zhang, Jianlin Feng, and Zheng Chen. “Knowledge graph embedding by translating on hyperplanes.” In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28, no. 1. 2014.
[8] Sun, Zhiqing, Zhi-Hong Deng, Jian-Yun Nie, and Jian Tang. “RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space.” In International Conference on Learning Representations. 2018.
[9] Cai, Hongyun, Vincent W. Zheng, and Kevin Chen-Chuan Chang. “A comprehensive survey of graph embedding: Problems, techniques, and applications.” IEEE Transactions on Knowledge and Data Engineering 30, no. 9 (2018): 1616-1637.
[10] Nickel, Maximillian, and Douwe Kiela. “Poincaré Embeddings for Learning Hierarchical Representations.” Advances in Neural Information Processing Systems 30 (2017): 6338-6347.
[11] Chami, Ines, Adva Wolf, Da-Cheng Juan, Frederic Sala, Sujith Ravi, and Christopher Ré. “Low-Dimensional Hyperbolic Knowledge Graph Embeddings.” In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pp. 6901-6914. 2020.
[12] Dettmers, Tim, Pasquale Minervini, Pontus Stenetorp, and Sebastian Riedel. “Convolutional 2d knowledge graph embeddings.” In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1. 2018.
[13] Wang, Quan, Pingping Huang, Haifeng Wang, Songtai Dai, Wenbin Jiang, Jing Liu, Yajuan Lyu, Yong Zhu, and Hua Wu. “Coke: Contextualized knowledge graph embedding.” arXiv preprint arXiv:1911.02168 (2019).
[14] Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. “Attention is All you Need.” In NIPS. 2017.
[15] Ali, Mehdi, Max Berrendorf, Charles Tapley Hoyt, Laurent Vermue, Mikhail Galkin, Sahand Sharifzadeh, Asja Fischer, Volker Tresp, and Jens Lehmann. “Bringing light into the dark: A large-scale evaluation of knowledge graph embedding models under a unified framework.” arXiv preprint arXiv:2006.13365 (2020).
[16] Berrendorf, Max, Evgeniy Faerman, Laurent Vermue, and Volker Tresp. “Interpretable and fair comparison of link prediction or entity alignment methods with adjusted mean rank.” arXiv preprint arXiv:2002.06914 (2020).
[17] Sun, Zhiqing, Shikhar Vashishth, Soumya Sanyal, Partha Talukdar, and Yiming Yang. “A Re-evaluation of Knowledge Graph Completion Methods.” In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pp. 5516-5522. 2020.
[18] Ruffinelli, Daniel, Samuel Broscheit, and Rainer Gemulla. “You can teach an old dog new tricks! on training knowledge graph embeddings.” In International Conference on Learning Representations. 2019.