Graph Neural Networks and KGs

Материалы Ссылка
Видео YouTube
Слайды pdf
Конспект здесь
Домашнее задание link

Видео

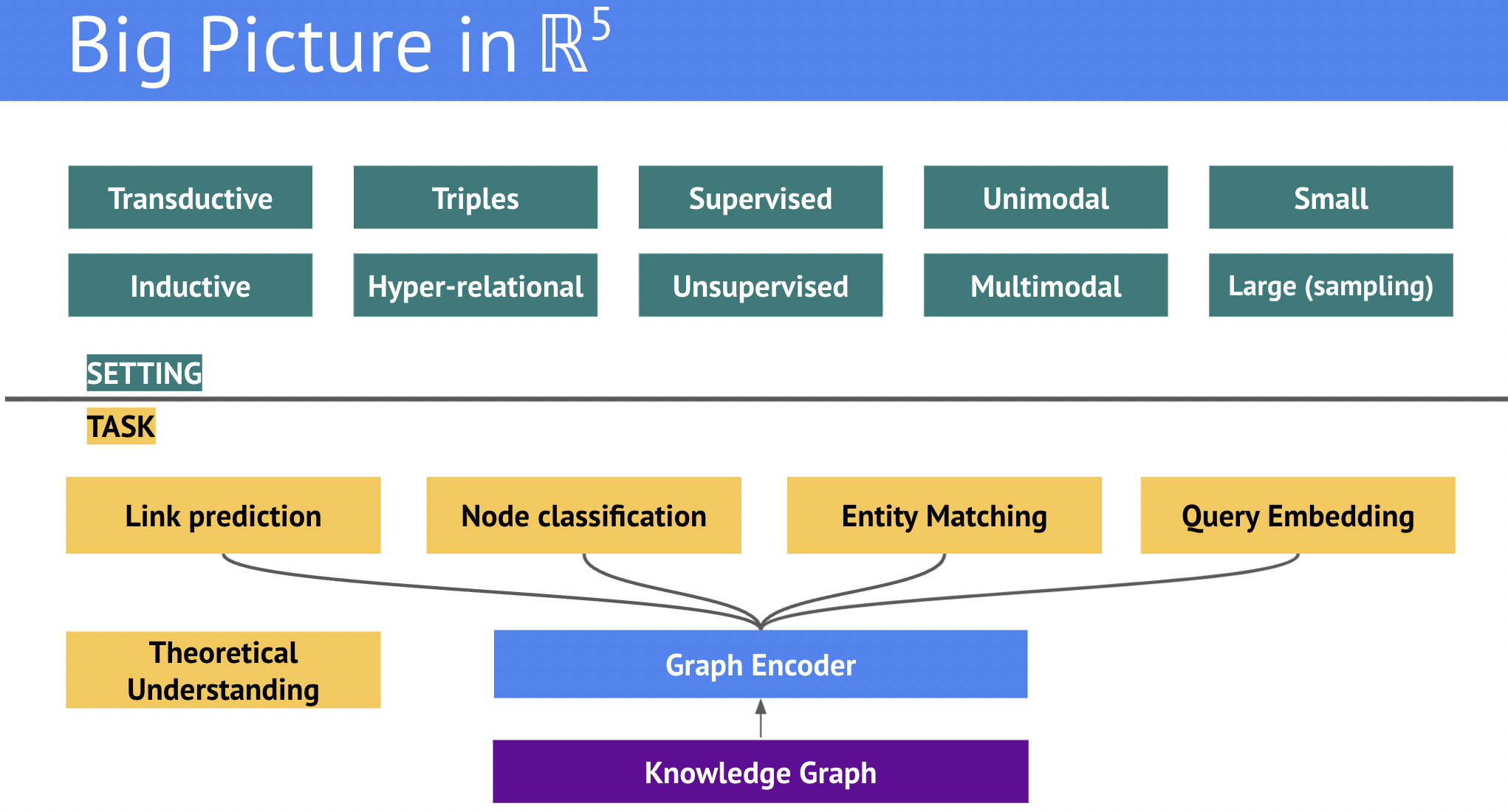
Graph Encoders

В предыдущей лекции мы рассматривали простые (shallow) decoder-only модели для векторных представлений KG и их использовании только в задаче предсказания связей (link prediction). Область машинного обучения на графах (Graph ML), однако, куда шире и позволяет решать множество других задач, в т.ч. классификацию вершин (node classification), классификацию графов (graph classification), регрессии вершин и графов (node regression, graph regression). Одним из мощных инструментов решения этих задач, который пригодится и в исследовании KGs являются графовые нейросети (Graph Neural Networks, GNNs), которые могут служить универсальным графовым энкодером для решения downstream задач.

Message Passing (передача сообщений) - один из подходов для построение и анализа GNNs. Большое количество GNN архитектур можно интерпретировать в контексте message passing, поэтому сперва стоит рассмотреть основы этой парадигмы. Содержимое этой лекции основано на нескольких книгах, Geometric Deep Learning protobook [0], Graph Representation Learning Book [1], где можно найти более подробные теоретические обоснования, выкладки и объяснения. Еще стоит отметить публикации в журнале Distill.pub [2].

В этой лекции мы рассмотрим концепцию message passing, как она работает на классических (не multi-relational) графах, основные семейства архитектур, а затем их усовершенствования для работы с KGs, которые отличаются (1) наличием типов связей; (2) частым отсутствием признаков вершин, из-за чего нужно обучать эмбеддинги вершин.

Inputs & Outputs

Прежде чем рассматривать конкретные имплементации, стоит договориться о формате ввода-вывода от ожидаемых архитектур:

Как правило, на вход графовым энкодерам в message passing подаются:

  • Матрица смежности (adjacency matrix) $A$ - часто для экономии памяти для графа из $N$ вершин вместо квадратной $N\times N$ матрицы используются разреженные матрицы (sparse matrix) или листы ребер (edge list).

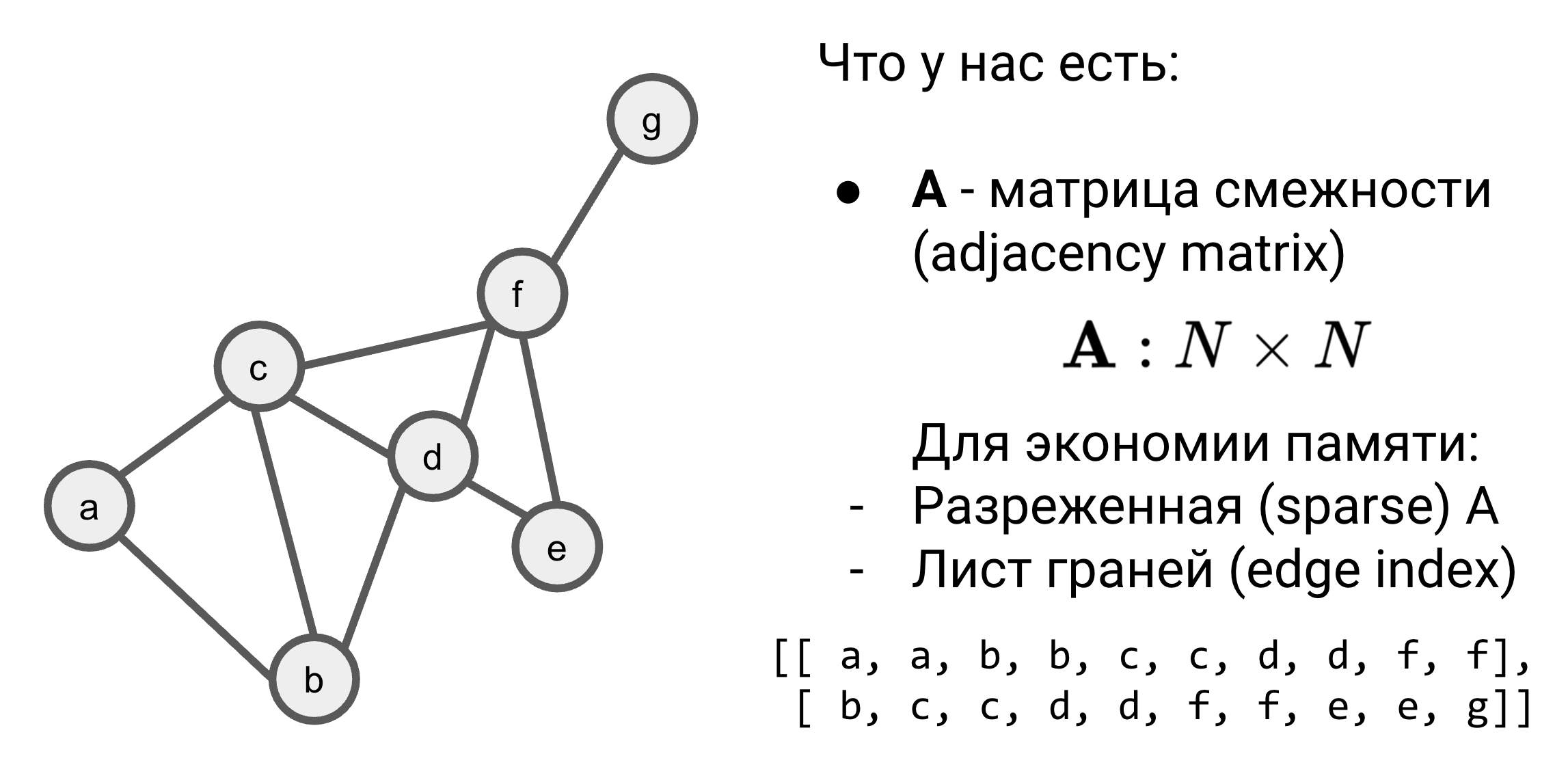
  • Признаки вершин (node features) $X\in \mathbf{R}^{|N|\times d}$ - которые могут быть заданными или обучаемыми эмбеддингами.
  • (Опционально) Признаки ребер (edge features) $E\in \mathbf{R}^{|E|\times d}$
  • (Опционально) Типы ребер (relation types) $R\in \mathbf{R}^{|R|\times d}$

На выходе процедуры message passing - обозначим ее функцией $f(.)$ - получаются обновленные представления всех признаков, поданных на вход:

  • $f(X) \rightarrow X’$
  • $f(E) \rightarrow E’$
  • $f(R) \rightarrow R’$

Обновленные представления из графового энкодера затем можно использовать в конкретной задаче, например, классификации вершин или предсказании связей, подключив подходящий декодер.

Message passing - не единственный способ строить графовые энкодеры и векторные представления, например, существуют и успешно применяются unsupervised методы (DeepWalk [3], node2vec [4], LINE [5], VERSE [6]). Тем не менее, из-за наличия многочисленных типов связей в KGs, message passing архитектуры получили более широкое применение в контексте работы с графами знаний.

Message Passing: Aggregate & Update

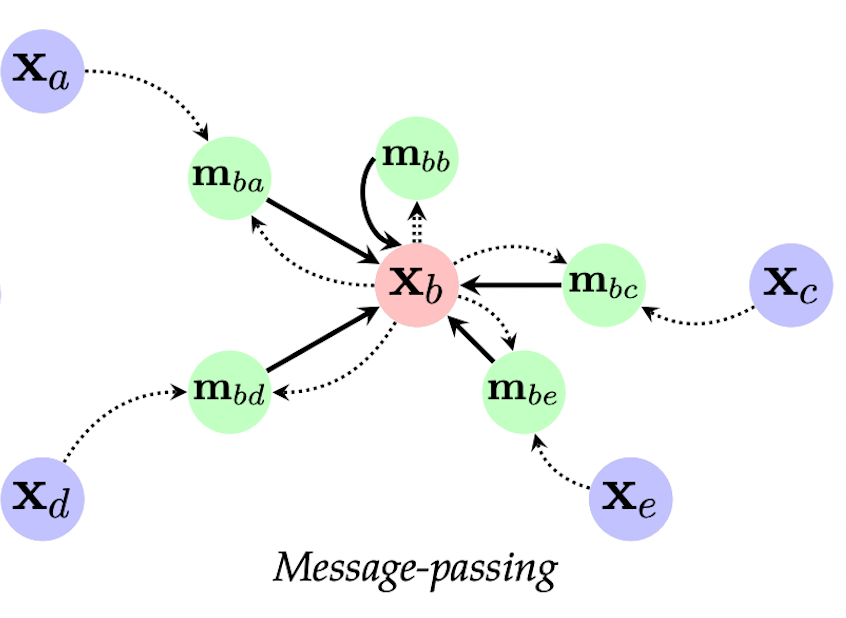
Идея message passing проста - вершины графа посылают сообщения, и новое представление каждой вершины получается как функция $\phi$ от:

  1. Предыдущего представления вершины
  2. Сообщений соседей

Эту функцию можно записать как:

\[ \mathbf{h}_{u} = \phi (\mathbf{x}_{u}, \mathbf{X}_{\mathcal{N}(u)}) \]

где $\mathbf{x}_u$ - предыдущее представление вершины $u$, $\mathbf{X}_{\mathcal{N}(u)}$ - представления соседей $u$, где $\mathcal{N}(u)$ обозначает сообщество вершины $u$. Другими словами, message passing выполняет процесс итеративной агрегации соседей (neighborhood aggregation).

Представление соседей получается путем как функция $\psi$ от представлений соседей:

\[ \mathbf{X}_{\mathcal{N}(u)} = \psi (\mathbf{x}_{n1}, \dots , \mathbf{x}_{nk}) \]

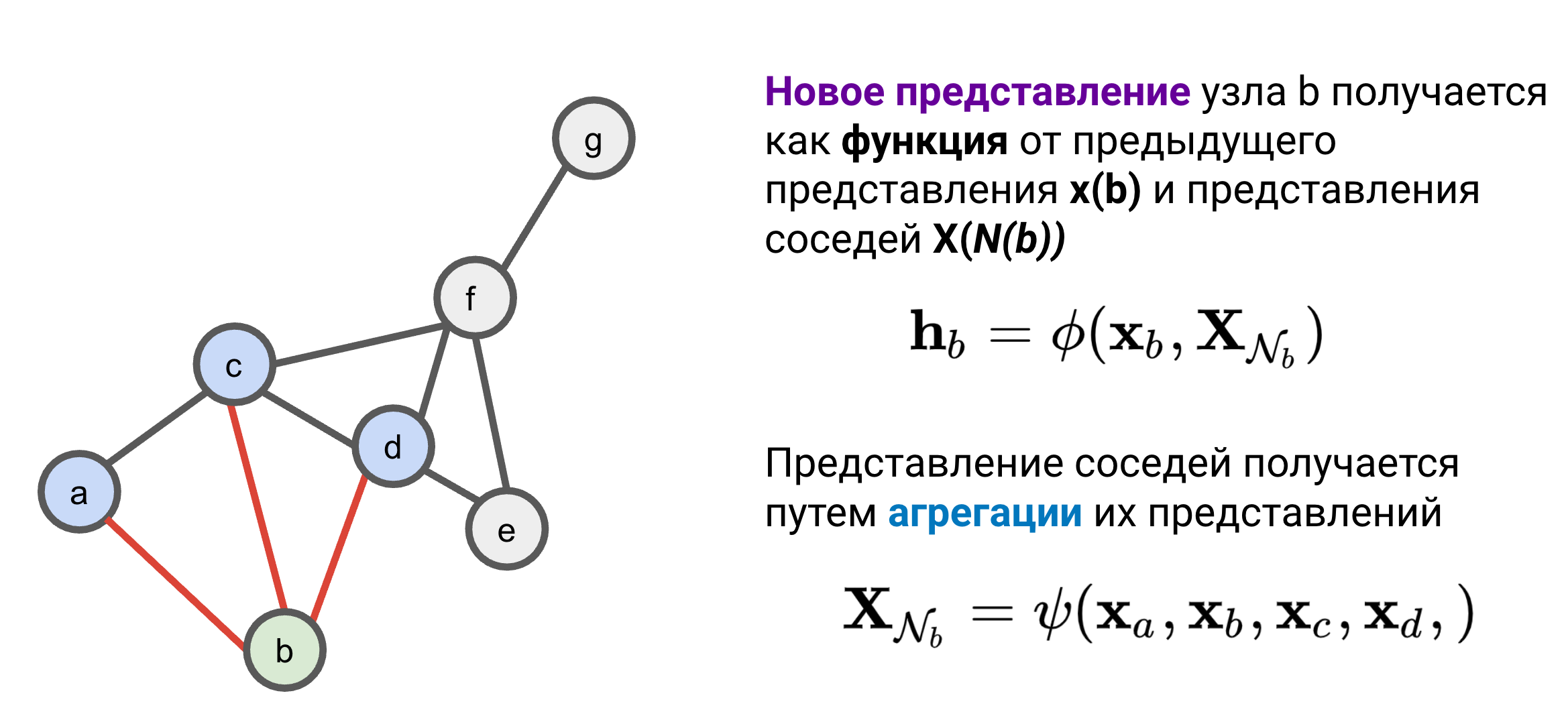
Для графа на рисунке для вершины $b$ представление соседей строится от представлений вершин $a$, $c$, $d$. Часто, для простоты в функцию $\psi$ добавляют и предыдущее представление рассматриваемой вершины $v$:

\[ \mathbf{X}_{\mathcal{N}(b)} = \psi (\mathbf{x}_a, \mathbf{x}_b, \mathbf{x}_c, \mathbf{x}_d ) \]

Концептуально, message passing состоит из двух шагов:

  1. Построение сообщения через агрегацию соседей (Aggregate)
  2. Обновление представления вершины (Update)

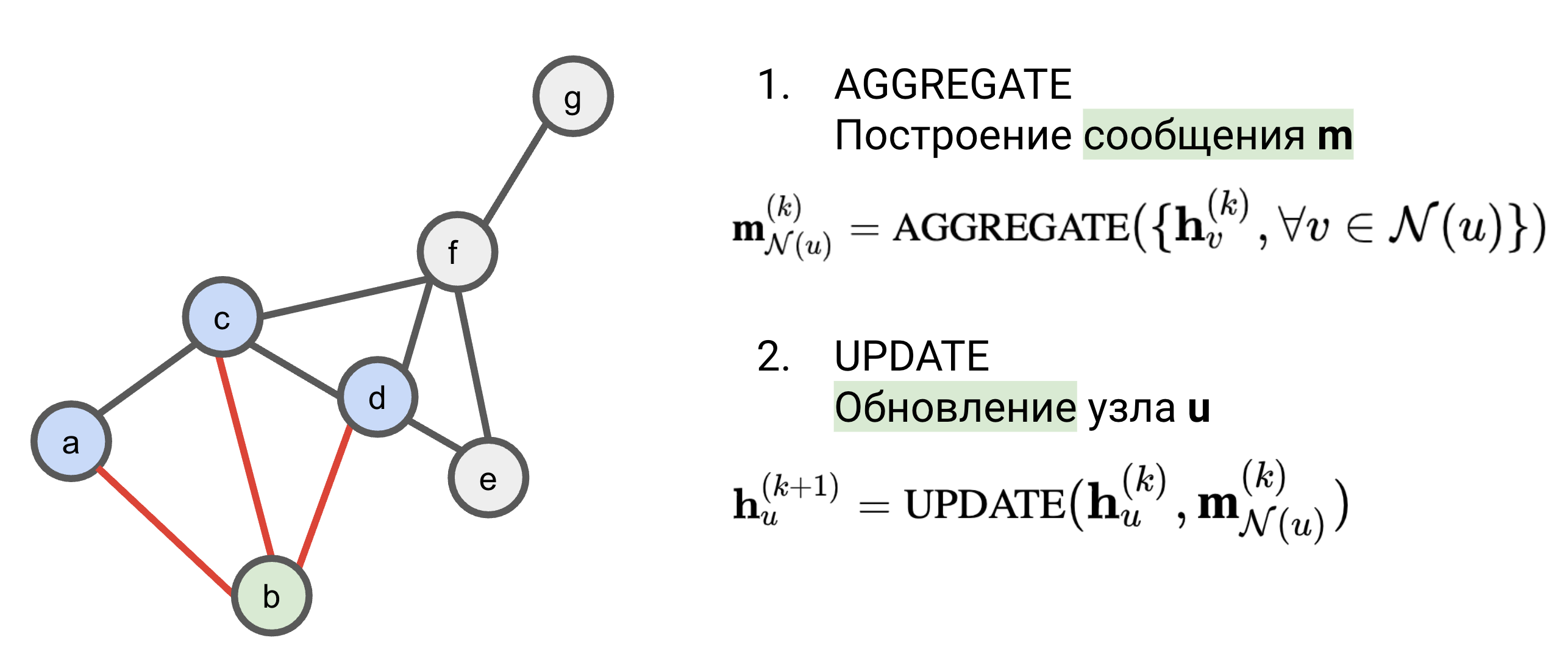
Шаг Aggregate

На первом шаге для вершины $u$ строится сообщение $\mathbf{m}_{\mathcal{N}(u)}$:

\[ \mathbf{m}_{\mathcal{N}(u)} = \text{AGGREGATE}( \{ \mathbf{h}_v, \forall v \in \mathcal{N}(u) \} ) \]

В графах нет простого понятия “местоположения” вершины, то есть мы не можем сказать, что вершина $u$ находится “справа” или “сверху” от вершины $v$. У каждой вершины есть сообщество соседей, которое мы можем в общем случае перечислять в любом порядке. Поэтому функция агрегации должна быть инвариантна к перестановкам (permutation invariance) - то есть результат агрегации не зависит от порядка ее применения к вершинам-соседям.

Мы будем записывать permutation invariant функции как $\bigoplus$ :

\[ \mathbf{m}_{\mathcal{N}(u)} = \bigoplus_{v \in \mathcal{N}(u)} \psi ( \mathbf{x}_v ) \]

Простые 4 функции, инвариантные к перестановке аргументов:

  • суммирование $\sum$
  • усреднение $avg()$
  • взятие минимального $min()$
  • взятие максимального $max()$

Например, часто используемое агрегирование через сумму представлений соседей и умножение с обучаемой весовой матрицей $\mathbf{W}_{\text{neigh}}$ будет записываться как:

\[ \mathbf{m}_{\mathcal{N}(u)} = \mathbf{W}_{\text{neigh}}\sum_{v \in \mathcal{N}(u)} \mathbf{x}_v \]

В зависимости от задачи, выбор инвариантной функции может заметно влиять на результат [7] - например, если в задаче определения изомрофизма двух графов с разным количеством вершин у всех вершин одинаковые признаки, то функции $avg(), min() , max()$ вернут одинаковые значения и только $sum()$ вернет уникальные значения. Еще можно использовать все инвариантные функции сразу и составлять сообщение как линейную комбинацию этих функций (метод Principal Neighborhood Aggregation, PNA) [8].

Шаг Update

Новое представление вершины $u$ на $k$-ом слое получается в результате функции UPDATE от предыдущего представления этой вершины $\mathbf{h}_u$ и сообщения $\mathbf{m}$, полученного на шаге AGGREGATE:

\[ \mathbf{h}_{u}^{(k+1)} = \text{UPDATE}( \mathbf{h}_u^k, \mathbf{m}_{\mathcal{N}(u)}^k ) \]

Или с использованием нотации агрегирования:

\[ \mathbf{h}_{u}^{(k+1)} = \phi( \mathbf{h}_u^k, \bigoplus_{v \in \mathcal{N}(u)} \mathbf{h}_v^k ) \]

В простейшем виде функция UPDATE может складывать преобразованные представления и пропускать результат через некоторую нелинейную функцию $\sigma$ (sigmoid, tanh, ReLU, и т.д.):

\[ \mathbf{h}_{u}^{(k+1)} = \sigma( \mathbf{W}_{\text{self}}\mathbf{h}_u^k + \mathbf{W}_{\text{neigh}} \mathbf{m}_{\mathcal{N}(u)}^k ) \]

где $\mathbf{W}_{\text{self}}$ - обучаемая весовая матрица предыдущего представления, $\mathbf{W}_{\text{neigh}}$ - весовая матрица агрегации соседей из шага AGGREGATE.

В целом, задача функции UPDATE - скомбинировать имеющиеся векторы в новое представление вершины, поэтому способов такой комбинации может существовать довольно много и иметь разную сложность (например, использовать реккурентные модули (GRU или LSTM) [9]).

Глубина Message Passing сетей

Message Passing эквивалентен агрегации соседних представлений, поэтому для получения сообщений от $k$-hop соседей (k-hop neighborhood) нужно как минимум $k$ слоев message passing.

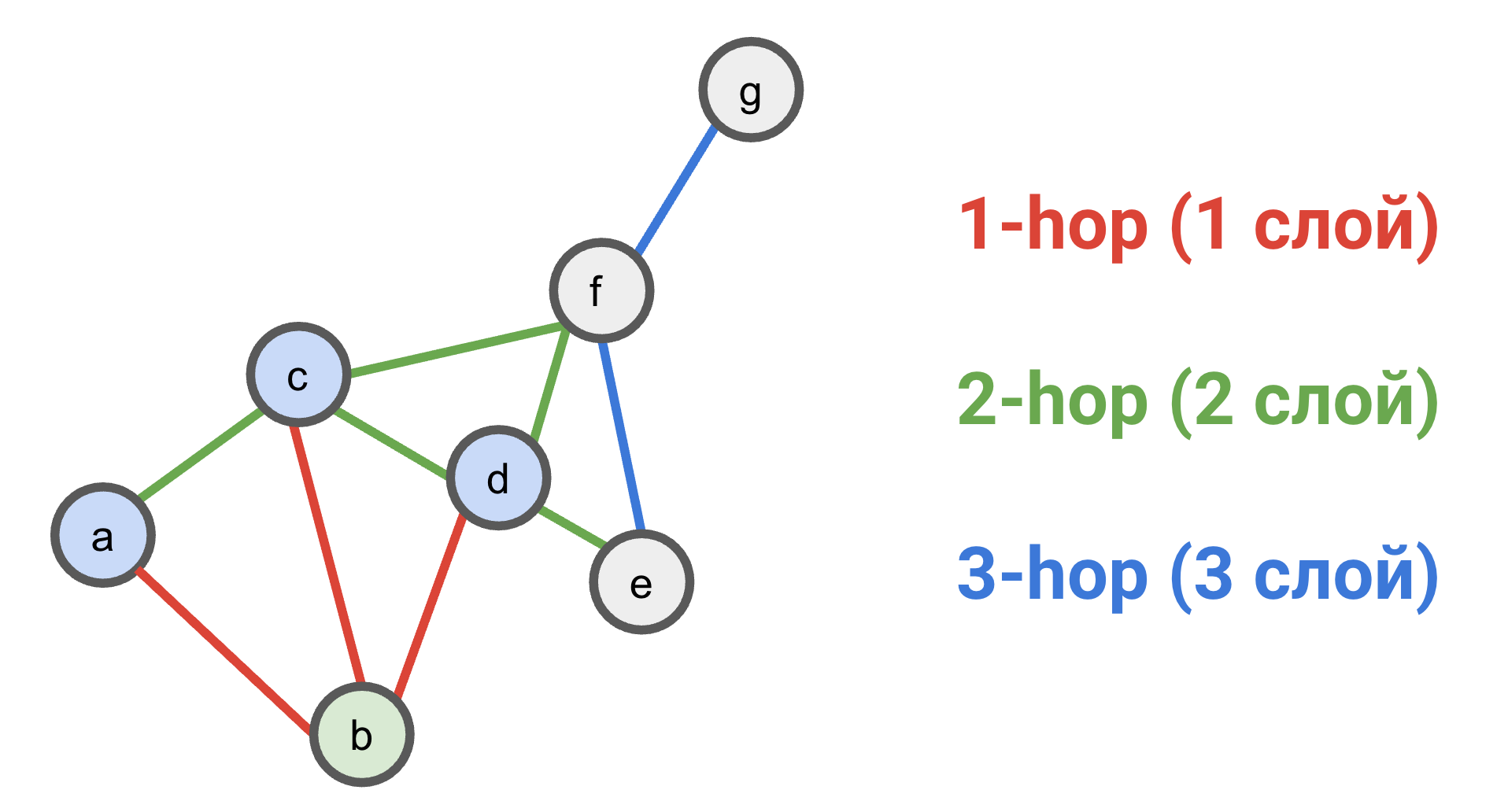Глубина получения сообщений с точки зрения вершины $b$

  • На первом слое вершина $b$ получает сообщения от непосредственных соседей $a$, $c$, $d$ (на первом слое представления вершин инициализированы только собственными признаками).
  • На втором слое вершина $b$ получит сообщения от вершин $e$ и $f$, так как их представления были агрегированы в вершины $d$ и $c$ на первом слое (вершины $a$, $c$, $d$ получают сообщения от своих соседей точно так же, как и вершина $b$).
  • На третьем слое вершина $b$ наконец получит сообщение от вершины $g$, чье представление было агрегировано в вершине $f$ на предыдущих слоях.

В общем случае, если мы хотим, чтобы каждая вершина получала сообщения от всех остальных вершин, то количество message passing слоев (глубина сети) должно быть не ниже диаметра графа.

Первые message passing архитектуры сильно теряли в качестве после 2-4 слоев [10] без дополнительных усовершенствований. Очень глубокие сети страдают от феноменов oversmoothing (представления вершин в сообществах размазываются и усредняются) [11] и oversquashing (слишком много информации от соседних вершин нужно уместить в один вектор) [12]. В настоящее время, сообщество нашло способы уменьшить эти негативные эффекты (например, помощью residual connections) и тренировать сети до 1000 слоев [13].

Матричная запись

Часто в литературе можно встретить матричную запись простых message passing архитектур, описывающую преобразования на уровне представлений всего графа. Если в нотации Aggregate & Update говорится о сообщениях, приходящих к конкретной вершине $u$, то в матричной записи покрывается весь граф.

Из линейной алгебры можно вспомнить, что произведение $AX$ разреженной матрицы смежности $A$ и матрицы признаков $X$ содержит для каждой вершины сумму представлений ее соседей, что является частным случаем message passing с инвариантным агрегатором суммирования.

Для того, чтобы включить в результирующее произведение представление самой вершины, вводят простую аугментацию - self-loops, то есть виртуальные ребра-петли, соединяющие каждую вершину саму с собой. В матричной записи петли (self-loops) описываются как identity matrix $I$ с единицами на главной диагонали. Тогда получается аугментированная матрица смежности:

\[ \tilde{A} = A + I \]

Полагая весовую матрицу агрегации соседей $\mathbf{W}_{\text{neigh}}$ равной весам агрегации предыдущего представления вершины $\mathbf{W}_{\text{self}}$, можно записать message passing на $k$-ом слое на уровне всего графа как уравнение:

\[ \mathbf{H}^{(k+1)} = \sigma (\mathbf{\tilde{A}}\mathbf{H}^{(k)}\mathbf{W}^{(k)}) \]

Различные GNN архитектуры усовершенствуют это уравнения дополнительной нормализацией (например, через степени вершин). Однако, не все архитектуры, например, такие как GAT, можно просто записать в матричной форме.

Message Passing Архитектуры

Концептуально, message passing архитектуры графовых нейросетей можно разделить на три семейства в зависимости от весов, которые назначаются ребрам в процессе агрегации соседних вершин.

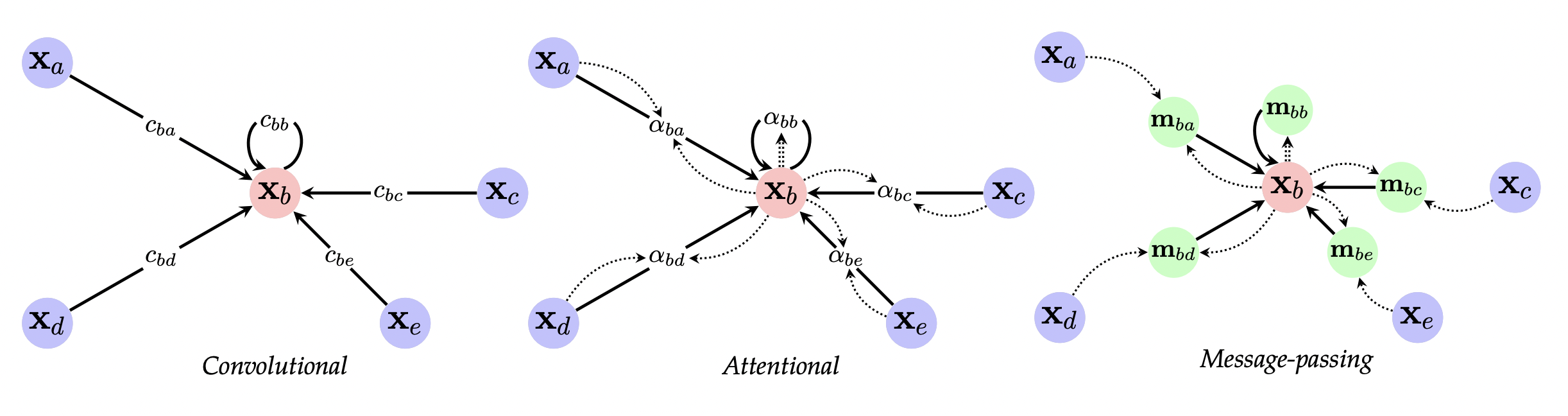Три основных семейства Message Passing архитектур. Источник [0]

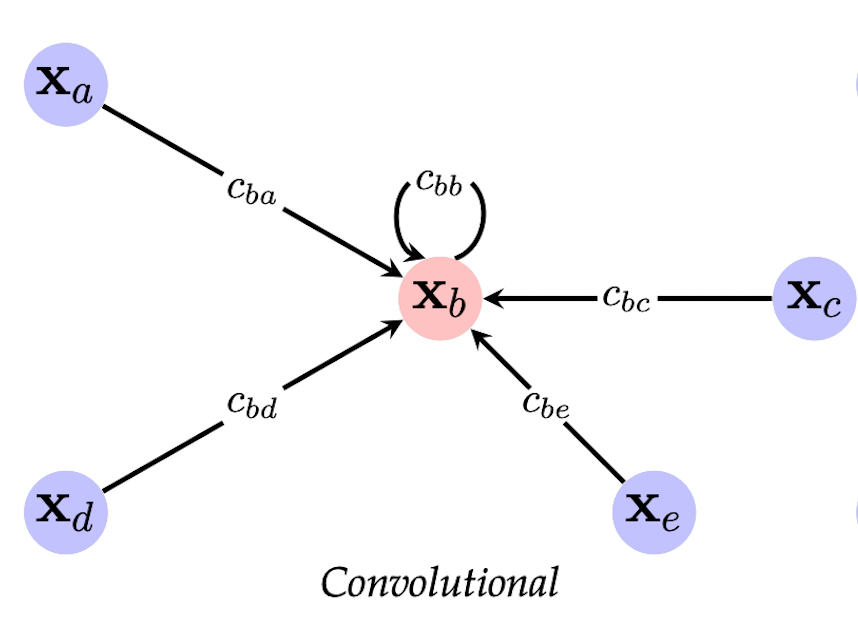
  • Графовые конволюционные сети (Graph Convolutional Nets, GCNs), у которых веса ребер это скаляры-константы, получающиеся из степеней вершин;
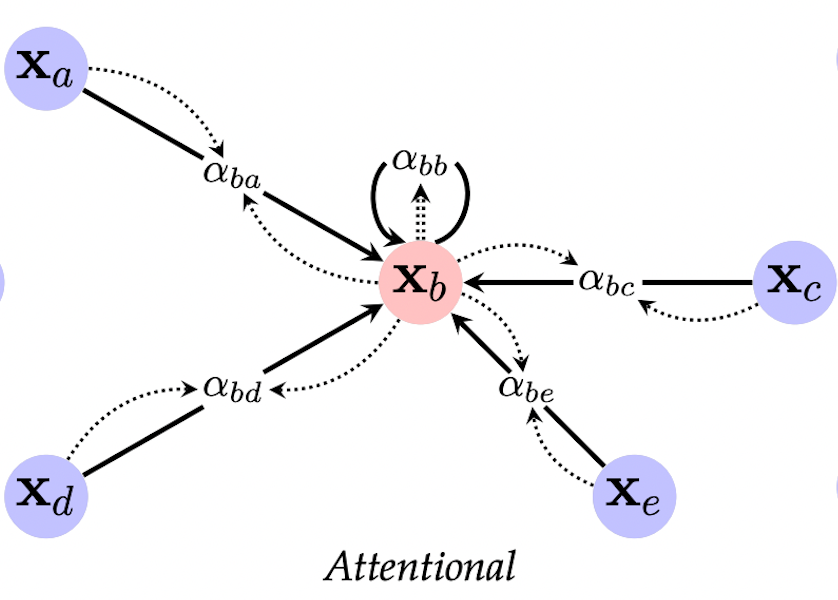
  • Графовые сети с вниманием (Graph Attention Nets, GATs), где веса - скаляры, но обучаемые в зависимости от представлений вершин;
  • Message-Passing графовые сети (Message-Passing Neural Nets, MPNNs), где веса ребер - векторы, которые объединяются с представлениями вершин через нелинейные функции.

Graph Convolutional Nets (GCN)

Источник [0]

В семействе конволюционных графовых сетей вес ребер при агрегации соседей константен. GCN [10] - не первая архитектура сверток на графах, но одна из самых известных, которая используется в огромном числе практических задач от компьютерного зрения и обработки естественного языка до физики и симуляций.

В парадигме message passing способ получения представления вершины записывается как:

\[ \mathbf{h}_i = \phi \Big( \mathbf{x}_i, \bigoplus_{j \in \mathcal{N}(i)} c_{ij} \psi (\mathbf{x}_j) \Big) \]

где $c_{ij}$ является скалярным весом ребра, соединяющего вершины $i$ и $j$. Разные GCN модели по-разному определяют этот вес как некоторую нормализационную константу. Классическая работа [10] определяет $c_{ij}$ как обратное от среднего геометрического степеней вершин $i$ и $j$:

\[ c_{ij} = \frac{1}{\sqrt{\vert \mathcal{N}(i) \vert \vert \mathcal{N}(j) \vert }} \]

Тогда UPDATE функция записывается как:

\[ \mathbf{h}_u^{(k)} = \sigma \Big( \mathbf{W}^{(k)} \sum_{v \in \mathcal{N}(u) \cup \{u\}} \frac{\mathbf{h}_v}{\sqrt{\vert \mathcal{N}(u) \vert \vert \mathcal{N}(v) \vert}} \Big) \]

Заметим, что в итерировании по соседям $v \in \mathcal{N}(u) \cup \{u\}$ мы добавляем саму вершину $u$, то есть добавляем петли self-loops.

В матричном виде нормализация использует аугментированную диагональную матрицу степеней вершин $\tilde{D}$, полученную из аугментированной матрицы смежности $\tilde{A} = A + I$.

\[ H = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}XW \]

Graph Attention Nets (GAT)

Источник [0]

В семействе графовых сетей с механизмом внимания вес ребер - по-прежнему скаляр, но обучаемый.

В парадигме message passing функцию UPDATE можно записать как:

\[ \mathbf{h}_i = \phi \Big( \mathbf{x}_i, \bigoplus_{j \in \mathcal{N}(i)} \alpha (\mathbf{x}_i,\mathbf{x}_j) \psi (\mathbf{x}_j) \Big) \]

где $\alpha(\mathbf{x}_i,\mathbf{x}_j)$ - обучаемый вес ребра.

Классическая работа по GAT [14] определяет этот весовой коэффициент через механизм внимания (attention) на основе представлений вершин и обучаемого вектора внимания $\mathbf{a}$:

\[ \alpha_{ij} = \frac{\text{exp} \Big( \text{LeakyReLU} \Big( \mathbf{a}^T [ \mathbf{W} h_i \vert\vert \mathbf{W} h_j ] \Big) \Big) }{\sum_{k \in \mathcal{N}_i} \text{exp} \Big( \text{LeakyReLU} \Big( \mathbf{a}^T [ \mathbf{W} h_i \vert\vert \mathbf{W} h_k ] \Big) \Big) } \]

где $\vert\vert$ - конкатенация, $\mathbf{a}^T$ - транспонирование. В этой формуле:

  • преобразованные представления вершин $h_i, h_j$ конкатенируются;
  • умножаются на attention vector;
  • преобразуются через LeakyReLU нелинейность;
  • пропускаются через softmax по всем ребрам к соседям вершины $i$.

Простой attention коэффициент приводит к следующей формуле функции UPDATE:

\[ h_i = \sigma \Big( \sum_{j \in \mathcal{N}_{i}} \alpha_{ij} \mathbf{W} h_j \Big) \]

Как и в любом механизм внимания, можно обучать несколько коэффициентов (attention heads) на каждое ребро, тогда на последнем шаге при получении представлений нужно сконкатанерировать представления от $K$ attention heads:

\[ h_i = \Big\vert\Big\vert_{k=1}^K \sigma \Big( \sum_{j \in \mathcal{N}_{i}} \alpha_{ij}^k \mathbf{W}^k h_j \Big) \]

В message passing сетях сообщения передаются по ребрам (в общем случае весьма разреженных) графов. Можно заметить, что архитектура трансформеров (Transformer) [16] является частным случаем GAT на полносвязном графе, когда каждая вершина соединена со всеми остальными.

Message Passing Neural Nets (MPNN)

Источник [0]

Самое общее семейство сетей [15], в котором у ребер тоже могут быть векторные признаки (edge features), заданные или обучаемые, которые участвуют с составлении сообщения наряду с представлениями вершин. Это можно записать в виде функции UPDATE:

\[ \mathbf{h}_i = \phi \Big( \mathbf{x}_i, \bigoplus_{j \in \mathcal{N}(i)} \psi (\mathbf{x}_i, \mathbf{x}_j) \Big) \]

Та же формула, если явно добавить $e_{ij}$ - edge feature ребра $i,j$:

\[ \mathbf{h}_i = \phi \Big( \mathbf{x}_i, \bigoplus_{j \in \mathcal{N}(i)} \psi (\mathbf{x}_i, \mathbf{x}_j, \mathbf{e}_{ij}) \Big) \]

Применительно к KGs, MPNN архитектура подходит больше, чем GCNs и GATs, так как многочисленные предикаты (relation types) и их обучаемые эмбеддинги могут быть представлены как edge features.

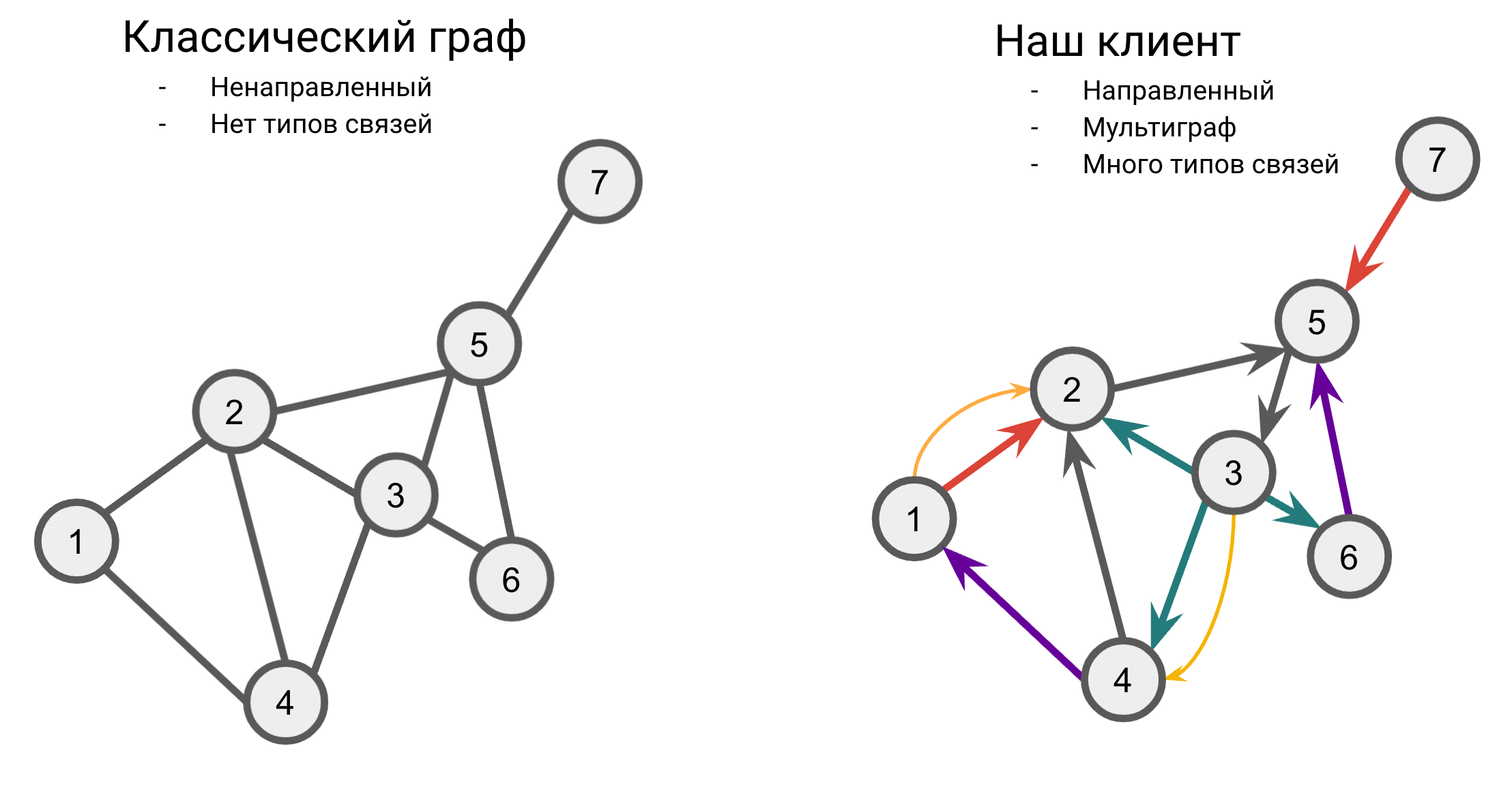
В этой главе мы рассматривали архитектуры, применяющиеся к классическим графам - ненаправленным и без типов связей. KGs, в свою очередь, являются направленными мультиграфами с большим количеством типов связей, поэтому стандартные GCN / GAT архитектуры в изначальном виде неприменимы, и нужно искать способы их адаптации к таким графам.

Relational GCNs (R-GCN)

Одной из первых GNN архитектур для multi-relational графов, KGs в том числе, стала R-GCN [17] (Relational GCN), прямая адаптация модели GCN от самих авторов.

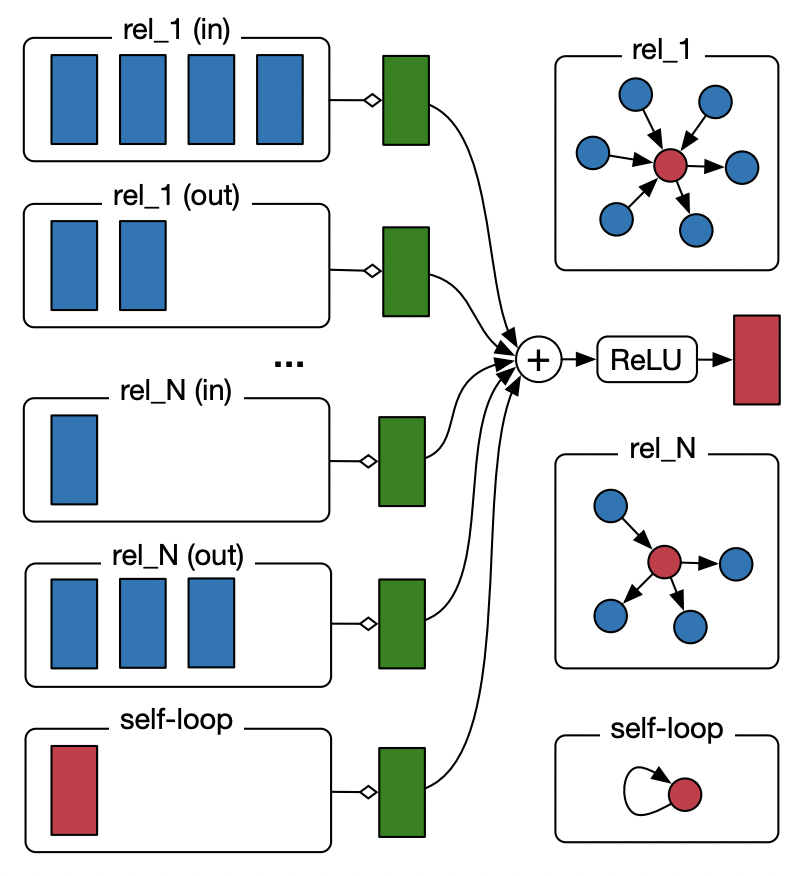
Новшества R-GCN в сравнении с GCN:

  • Граф из $\vert R \vert$ предикатов разбивается на $\vert R \vert$ подграфов, где каждый подграф содержит ребра только одного типа
  • Каждый тип связи $r$ имеет собственную весовую матрицу $\mathbf{W}_r$
  • Нормализация считается по $r$-подграфу

Источник [17]

Рисунок иллюстрирует способ работы R-GCN: по каждому $r$-ному подграфу применяется классический GCN слой с собственной весовой матрицей типа связи. Заметим, что в каждом подграфе отдельно обрабатываются два вида направленных ребер - входящие (incoming) и исходящие (outgoing). Таким образом, общее количество типов связи увеличивается в два раза (на рисунке тип связи rel_1 (in) отличается от типа связи rel_2 (out)). Вспомогательные петли (self-loops) тоже описаны как уникальный тип связи.

В парадигме message passing шаг UPDATE в R-GCN можно записать как:

\[ \mathbf{h}_i = \sigma \Big( \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}^r_i} \frac{1}{c_{i,r}} W_r h_j + W_0 h_i \Big) \]

где $\sum_{r \in \mathcal{R}}$ говорит об отдельном процессе message passing для каждого $r$-ного подграфа с последующим суммированием, $j \in \mathcal{N}^r_i$ указывает, что в качестве соседей вершины $i$ будут браться только соседи одного типа $r$. $c_{i,r}$ - нормализационная константа, которая считается точно так же, как и в GCN, но по $r$-ному подграфу. $W_{r}$ - весовая матрица для каждого типа связи и $W_{0}$ - весовая матрица для агрегирования предыдущего представления вершины $i$.

Декомпозиция и представление графа

Рассмотрим подробнее процесс декомпозиции исходного графа.

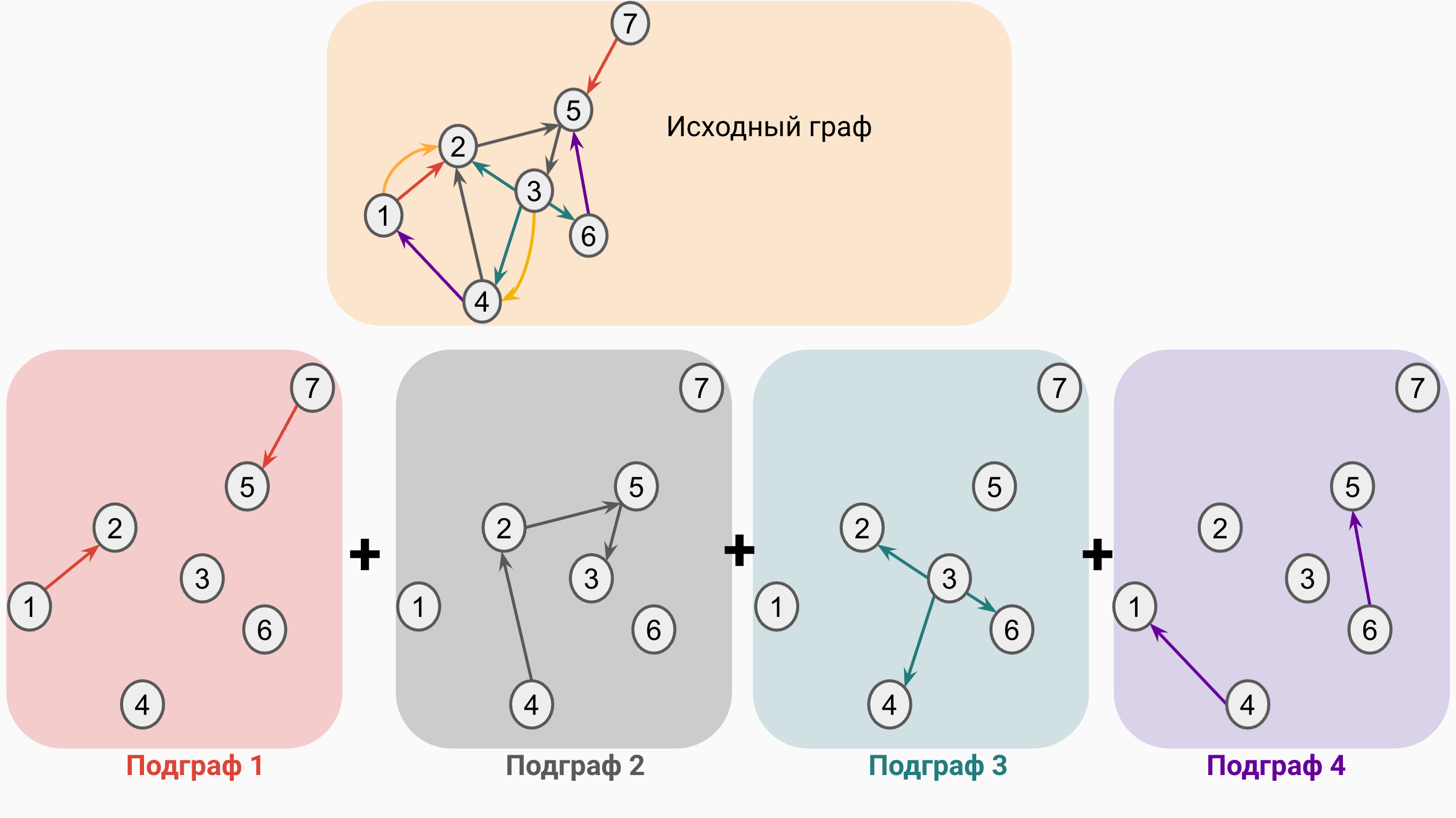
В исходном графе содержится 5 типов ребер, для простоты на рисунке отражено 4. Каждый $r$-ный подграф содержит ребра только одного типа $r$. Таким образом, Подграф 1 будет состоять только из двух ребер, Подграф 2 из трех ребер, и так далее. Хотя в каждом подграфе и может появиться множество несвязных (disconnected) вершин, message passing по ним в данном подграфе проводиться не будет.

Каждый подграф можно описать двумя способами:

  1. Разреженная матрица смежности (sparse adjacency matrix), например в COO или CSR форматах.
  2. Лист ребер (edge list). Например, edge list подграфа 1 содержит ребра $1 \rightarrow 2$ и $7 \rightarrow 5$ и будет иметь размерность [2, num_edges_r]:
[[1, 7],  # source nodes
 [2, 5]]  # target nodes

В результате, для $\vert R \vert $ подграфов мы будем хранить $\vert R \vert$ разреженных матриц или edge lists.

Базисная декомпозиция весов предикатов

В R-GCN каждый тип связи параметризуется обучаемой матрицей $W_r$. Это приводит к быстрому росту общего числа обучаемых параметров и ведет к переобучению. Для уменьшения этих негативных эффектов авторы предлагают вместо обучения $\vert R \vert$ матриц рассматривать эти весовые матрицы как линейную комбинацию некоторого фиксированного числа $B$ базисных матриц.

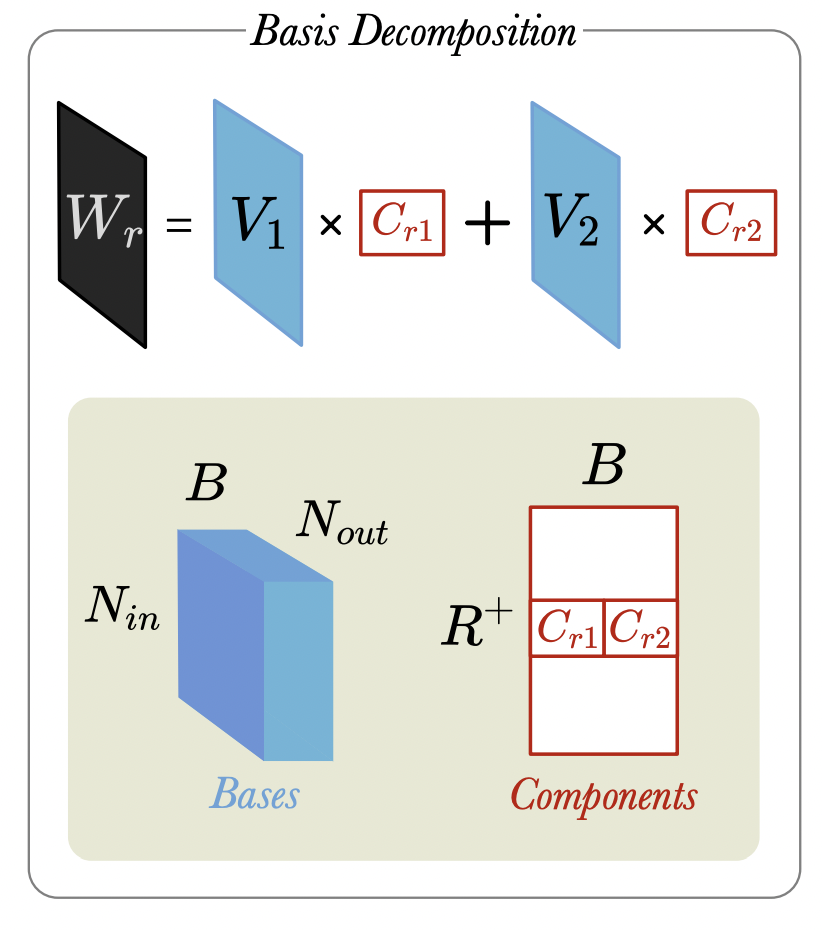Источник [18]

Интуитивно, каждая базисная матрица представляет некоторый неинтерпретируемый прототип типа связи, комбинируя которые можно получать конкретные предикаты данного KG. Как правило, число $B$ базисных матриц задается заранее.

\[ \mathbf{W}_r = \sum_{i=1}^{b} \alpha_{i,r} \mathbf{B}_{i} \]

где $\alpha_{i,r}$ - обучаемые скалярные коэффициенты линейной комбинации для каждого уникального предиката в графе.

С учетом базисной декомпозиции предикатов и нормализации функцию message $\mathbf{m}$ можно записать как:

\[ \mathbf{m}_{\mathcal{N}(u)} = \sum_{r \in \mathcal{R}} \sum_{v \in \mathcal{N}_r(u)} \frac{\mathbf{\alpha}_r \times_1 \mathbf{B} \times_2 \mathbf{h}_v }{f_n (\mathcal(N)(u), \mathcal{N}(v))} \]

где $\mathbf{\alpha}_r$ - вектор скалярных коэффициентов, $f_n$ - константа нормализации, $\times_k$ - умножение по моде $k$.

Декодеры

R-GCN - графовый энкодер, который возвращает обновленные представления вершин и матрицы предикатов. Для выполнения конкретной задачи (классификации или предсказания связей) R-GCN нужно связать с конкретным декодером, выход которого соответствует задаче.

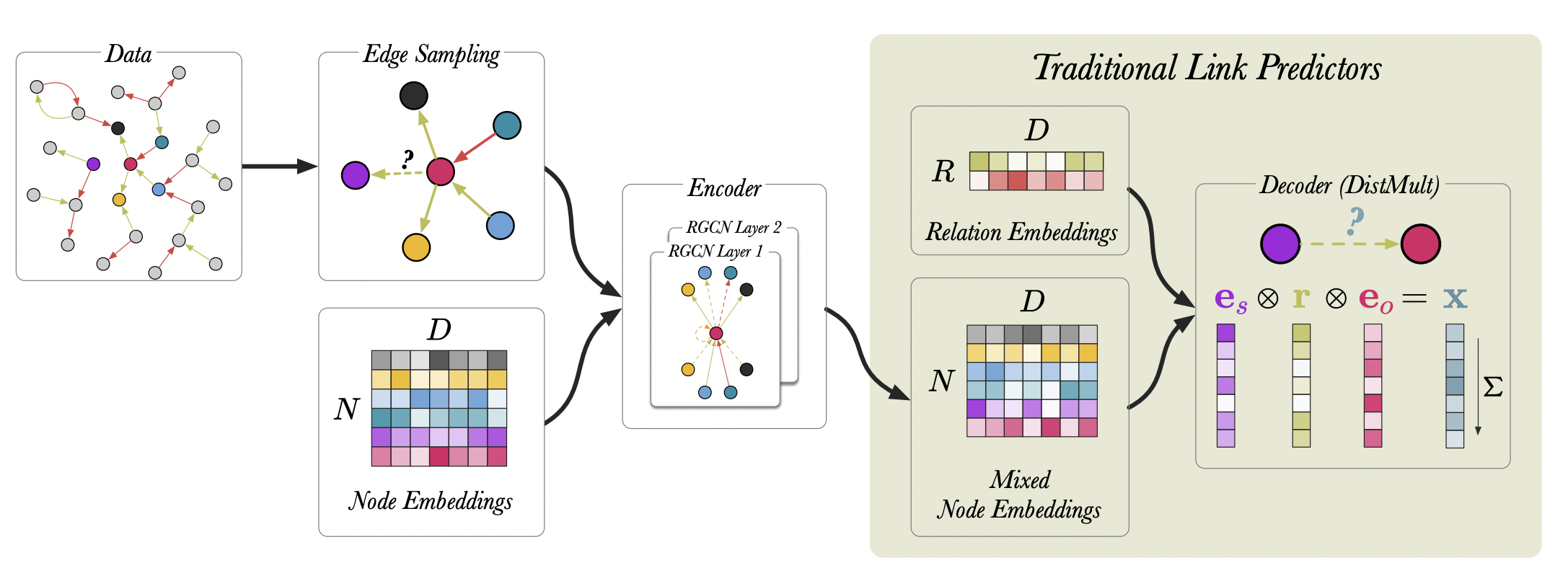Источник [18]

  • Векторы вершин - выход R-GCN;
  • Векторы типов связей - ?

В случае предсказания связей (link prediction) нам нужно оценивать вероятность корректности того или иного триплета $(s,r,o)$, а значит в качестве декодера можно взять любую scoring function из предыдущей лекции, например TransE или DistMult. Представления вершин $s$ и $o$ можно взять напрямую из представлений R-GCN. Вспомним, однако, что для предикатов (типов связей) R-GCN обучает матрицы $\mathbf{W}_r \in \mathbb{R}^{d \times d}$, а не векторы $\mathbf{r} \in \mathbb{R}^{d}$, которые нужны в декодере. Поэтому в задаче link prediction, где используется R-GCN, нужно обучать дополнительные эмбеддинги типов связей, где каждому типу связи соответствует вектор, а не матрица.

Compositional GCNs (CompGCN)

Новая архитектура композиционных GCN, compositional GCNs (CompGCN) [19], призвана решить проблему слишком сильной параметризации (overparameterization) R-GCNs. Концептульано, CompGCN ближе к MPNN архитектуре, так как предлагает использовать тип ребер при построении сообщений как композицию представлений вершины и ребра.

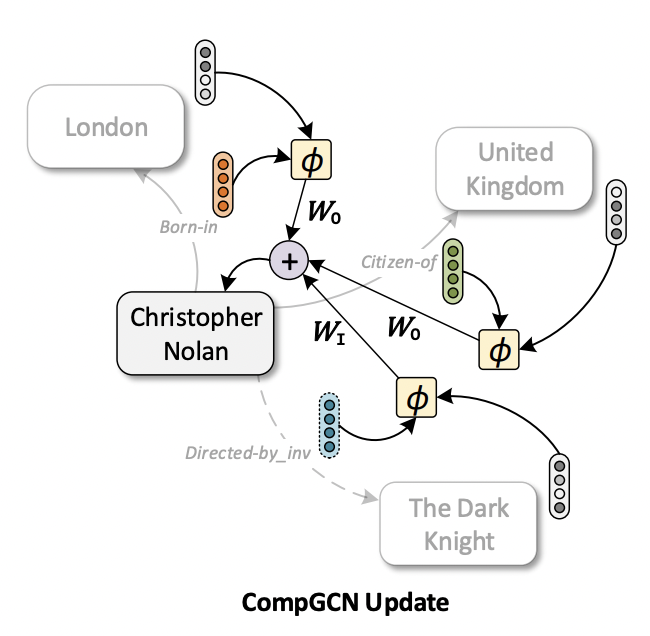Источник [19]

Преимущества CompGCN:

  • Типы связей параметризуются вектором $\mathbf{z}_r \in \mathbb{R}^d$, а не матрицами $\mathbf{W}_r$ ;
  • Тип связи участвует в построении сообщений как edge feature в композиции с вектором вершины;
  • Вместо $\vert R \vert$ только три обучаемые матрицы предикатов, отвечающие за направление ребра.

Пример составления сообщения представлен на схеме. Рассмотрим ребро (Nolan, born in, London). Теперь, когда вершины и ребра параметризуются векторами, CompGCN может строить общее векторное представление пары (born in, London) как композицию $\phi$ соответствующих векторов. Новое представление преобразуется весовой матрицей $\mathbf{W}_O$ как исходящее ребро (outgoing) и агрегируется с сообщениями от других соседей, составленных по тому же принципу.

Функция UPDATE в CompGCN записывается как:

\[ \mathbf{h}_v = f \Big( \sum_{(u, r) \in \mathcal{N}(v)} \mathbf{W}_{\lambda(r)} \phi (\mathbf{x}_u, \mathbf{z}_r) \Big) \]

где $\mathbf{W}_{\lambda(r)}$ - весовая матрица направлений ребер, которая принимает только три значения:

  • $\mathbf{W}_{O}, r \in \mathcal{R}$ для исходных ребер,
  • $\mathbf{W}_{I}, r \in \mathcal{R}_{inv}$ для инверсных ребер,
  • $\mathbf{W}_{\text{self-loop}}, r = \text{self-loop}$ для петель self-loops.

Так как в графе присутствуют все три типа ребер, то финальные сообщения получаются как среднее арифметическое от трех message passing вызовов:

\[ \mathbf{h}_v = \frac{1}{3} f \Big( \sum_{\lambda \in (I, O, SL)} \sum_{(u, r) \in \mathcal{N}(v)} \mathbf{W}_{\lambda(r)} \phi (\mathbf{x}_u, \mathbf{z}_r) \Big) \]

Composition function

Основное отличие CompGCN - типы ребер (предикаты) параметризуются вектором и поэтому могут быть включены в сообщение наряду с представлением вершины через функцию композиции $\phi (\mathbf{x}_u, \mathbf{z}_r)$. Задача этой функции - составить один вектор из двух, поэтому можно применять как параметрические функции (MLP), так и непараметрические. Авторы CompGCN предалагают использовать все многообразие непараметрических scoring functions из KG embedding алгоритмов, например:

  • TransE: $\phi (\mathbf{x}_u, \mathbf{z}_r) = \mathbf{x}_u + \mathbf{z}_r$
  • DistMult: $\phi (\mathbf{x}_u, \mathbf{z}_r) = \mathbf{x}_u * \mathbf{z}_r$
  • RotatE: $\phi (\mathbf{x}_u, \mathbf{z}_r) = \mathbf{x}_u \circ \mathbf{z}_r$

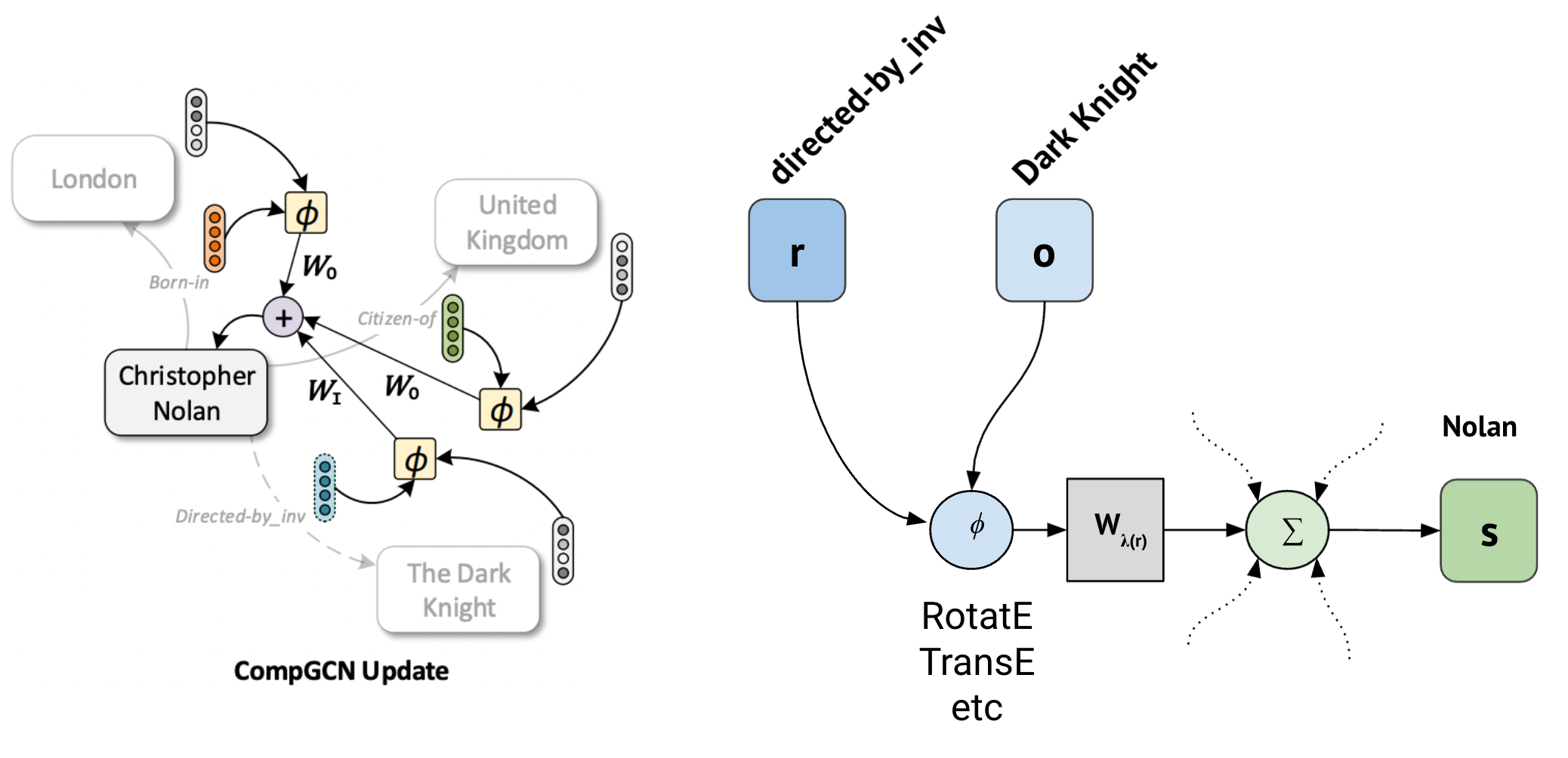
Если описать последовательность операций при составлении сообщения (на рисунке выше), то

  1. Сначала к паре (вершина, тип ребра) применяется функция композиции $\phi$,
  2. Затем результат пропускается через одну из трех весовых функий направления ребра $\mathbf{W}_{\lambda(r)}$,
  3. Затем векторы агрегируются с помощью permutation invariant оператора (например, суммы):

Эту процедуру CompGCN повторяет три раза для всех входящих, исходящих и вспомогательных петлевых (self-loops) ребер.

Формат описания графа

Формат ввода R-GCN предполагает разбиение графа на $\vert R \vert$ разных листов ребер (edge indices), каждый размером [2, num_edges_r]. CompGCN предложил более простой способ представления графа - в виде одного листа (edge index) [3, num_edges], где третья строка COO матрицы содержит типы ребер.

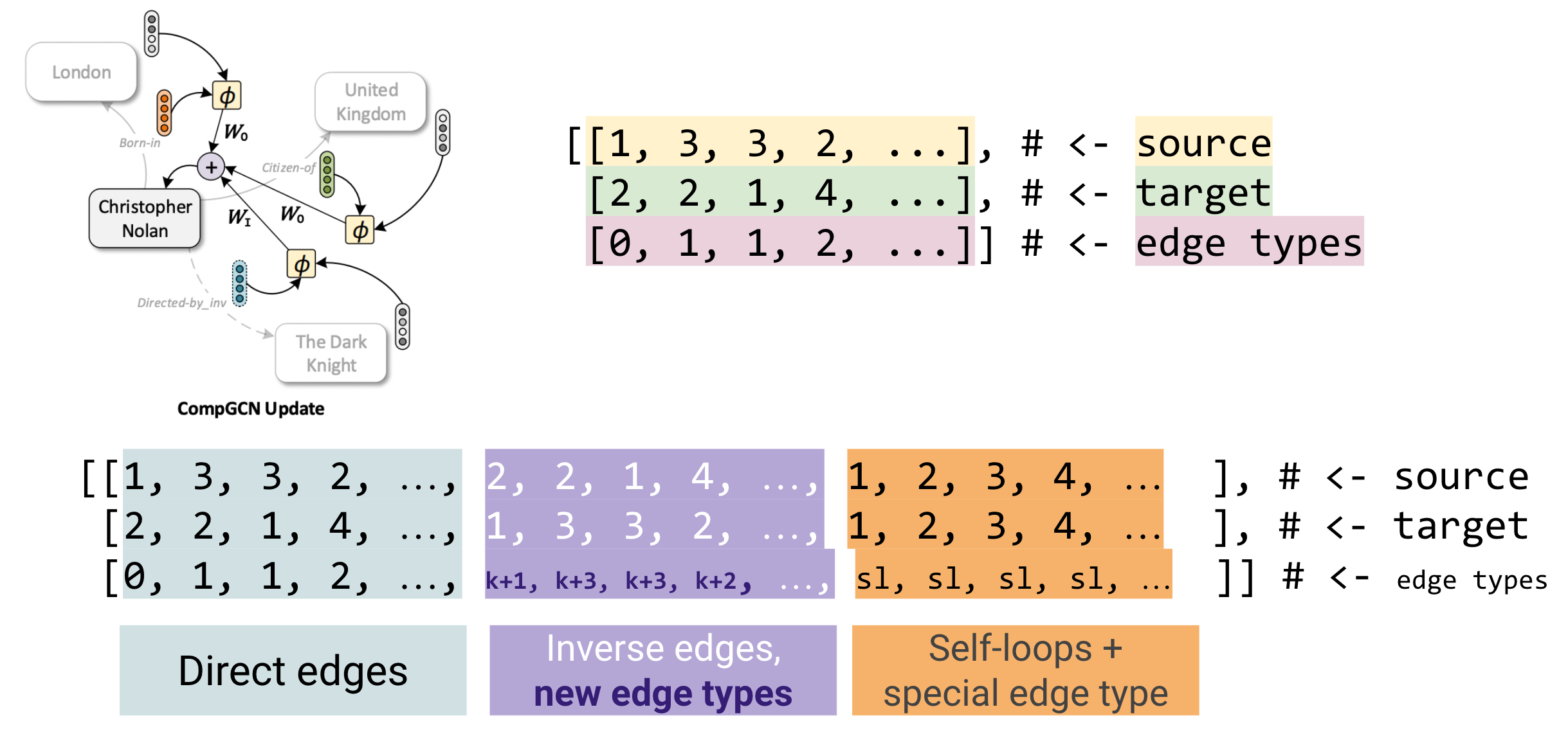
Например, существует 4 ребра в записи $(s, r, o)$

1, 0, 2
3, 1, 2
3, 1, 1
2, 2, 4

Тогда edge list из 4 исходящих ребер, 4 инверсных ребер и 4 ребер-петель (по числу уникальных вершин) будет записываться как

[[1, 3, 3, 2, 2, 2, 1, 4, 1, 2, 3, 4],
 [2, 2, 1, 4, 1, 3, 3, 2, 1, 2, 3, 4],
 [0, 1, 1, 2, k+1, k+2, k+2, k+3, sl, sl, sl, sl ]]

Декодеры

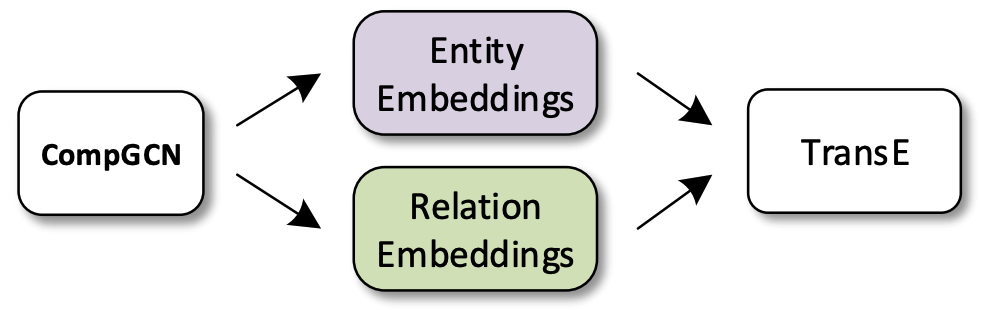
CompGCN как графовый энкодер возвращает векторы вершин и предикатов, и поэтому эти обновленные представления могут быть декодированы любой scoring function из семейства KG embeddings. Авторы экспериментировали с непараметрическими TransE, DistMult и параметрическим ConvE.

Inductive Learning

Во всей Лекции 7 и первой части этой лекции мы делали важное допущение: исходный граф (в частности, его вершины) во время тренировки и инференса (валидации, тестирования) не изменяет множества вершин. Другими словами, все вершины на инференсе находятся и в тренировочном наборе. Такой процесс инференса называется трансдуктивным (transductive).

В реальных задачах это допущение часто не выполняется - на инференсе появляются новые вершины (unseen nodes) или целые новые графы, которых нет в тренировочном наборе (seen nodes). Такой процесс вывода называется индуктивным (inductive). Выделяют минимум два подвида индуктивных сценариев:

  • Out-of-sample (вне выборки) - новые вершины на инференсе присоединяются к известному тренировочному графу;
  • Fully inductive (полностью индуктивный) - на инференс приходит абсолютно новый граф из новых вершин (но часто с известными типами ребер).
Трансдуктивный Индуктивный
Весь граф известен во время тренировки Новые вершины и графы на инференс
Применимы shallow embedding модели Shallow модели не могут выучить признак неизвестной вершины
Тренированные эмбеддинги применимы на инференсе Нужно строить признако вершин

Основной вопрос индуктивных сценариев по сравнению с трансдуктивным: “Как строить признаки вершин?”

Обучение эмбеддингов вершин трансдуктивными способами (через shallow модели как TransE и подобные) имеет мало смысла, так как их просто не применить к неизвестным вершинам. Следовательно, нужен некоторый новый способ строить признаки известных и будущих неизвестных вершин. Inductive Learning - одна из быстрорастущих тем в области Graph Representation Learning и в этой части мы рассмотрим несколько подходов к индуктивным сценариям.

Out-of-Sample Learning

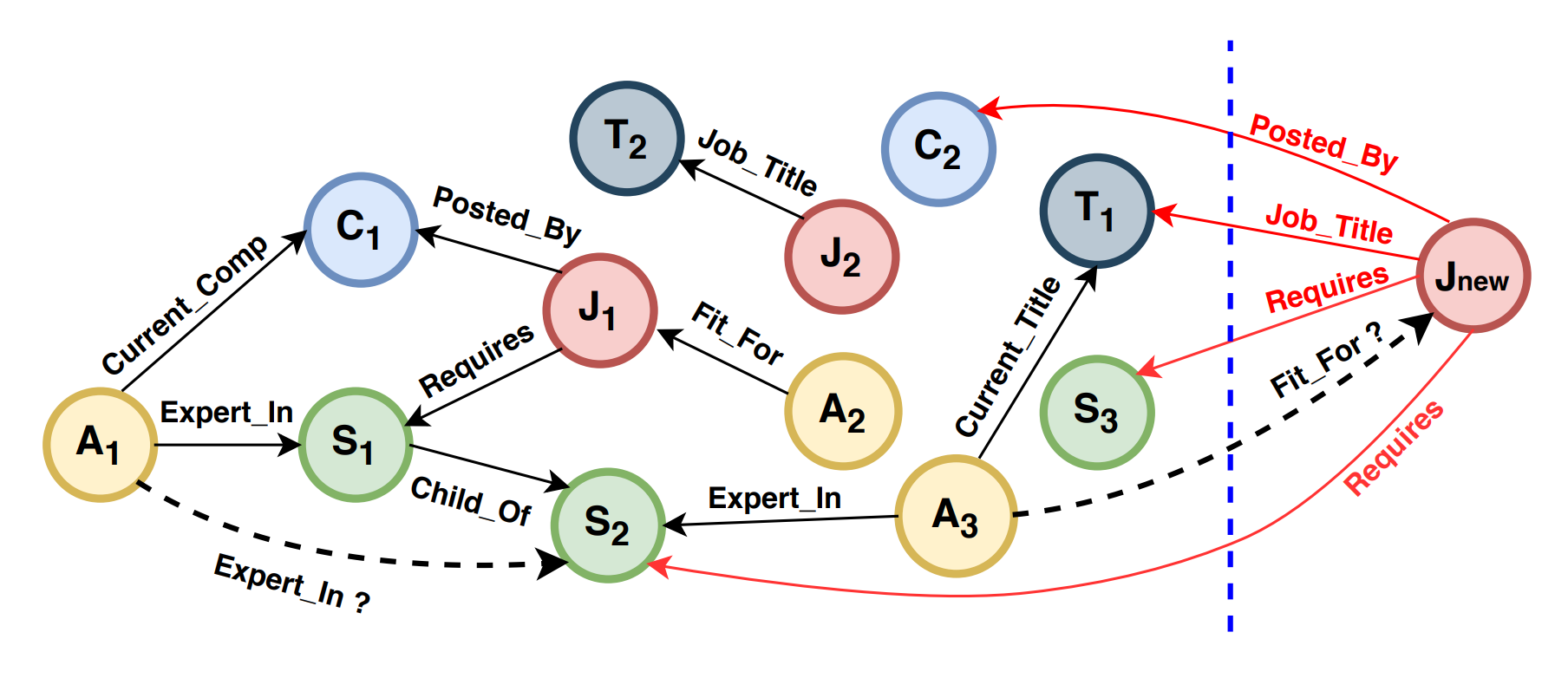Источник [20]

Сценарий Out-of-sample learning [20] предполагает, что к известному тренировочному графу $G = (\mathcal{V}, \mathcal{E}, \mathcal{R})$ c типами ребер $R$ присоединяется новая вершина $v \notin \mathcal{V}$. Другими словами, новая вершина приходит вместе с несколькими ребрами, и каждое ребро соединено с некоторой вершиной тренировочного графа:

\[ G_v = \{ (v, r, u): u \in \mathcal{V}, r \in \mathcal{R} \} \cup \{ (u,r,v): u \in \mathcal{V}, r \in \mathcal{R} \} \]

Задача out-of-sample сценария - предсказать новые ребра от (1) известного графа к новой вершине и (2) от новой вершины к известному графу.

Авторы оригинальной статьи [20] предложили использовать тренированные эмбеддинги вершин исходного графа для получения вектора признаков новых вершин как функцию от эмбеддингов известных соседей. В частности, применить DistMult к признакам каждой вершины и ребра и усреднить результат:

\[ \mathbf{z}_v = \frac{1}{\vert G_v \vert} \Big( \sum_{(v,r,u) \in G_v } \mathbf{z}_r \odot \mathbf{z}_u + \sum_{(u,r,v) \in G_v} \mathbf{z}_r \odot \mathbf{z}_u \Big)\]

С другой стороны, при таком способе постройки признаков нужно изменить стандартный трансдуктивный тренировочный процесс и симулировать во время тренировки прибытие неизвестных вершин. Авторы предлагают для этой цели новый тренировочный цикл со случайным шансом для каждого ребра стать ребром между известной и неизвестной вершинами. В первом случае будет использоваться стандартный DistMult, а во втором - новый способ агрегации соседних представлений.

Преимущества:

  • Можно использовать тренированные эмбеддинги вершин известного графа

Недостатки:

  • Нужен новый алгоритм тренировки

Textual Features

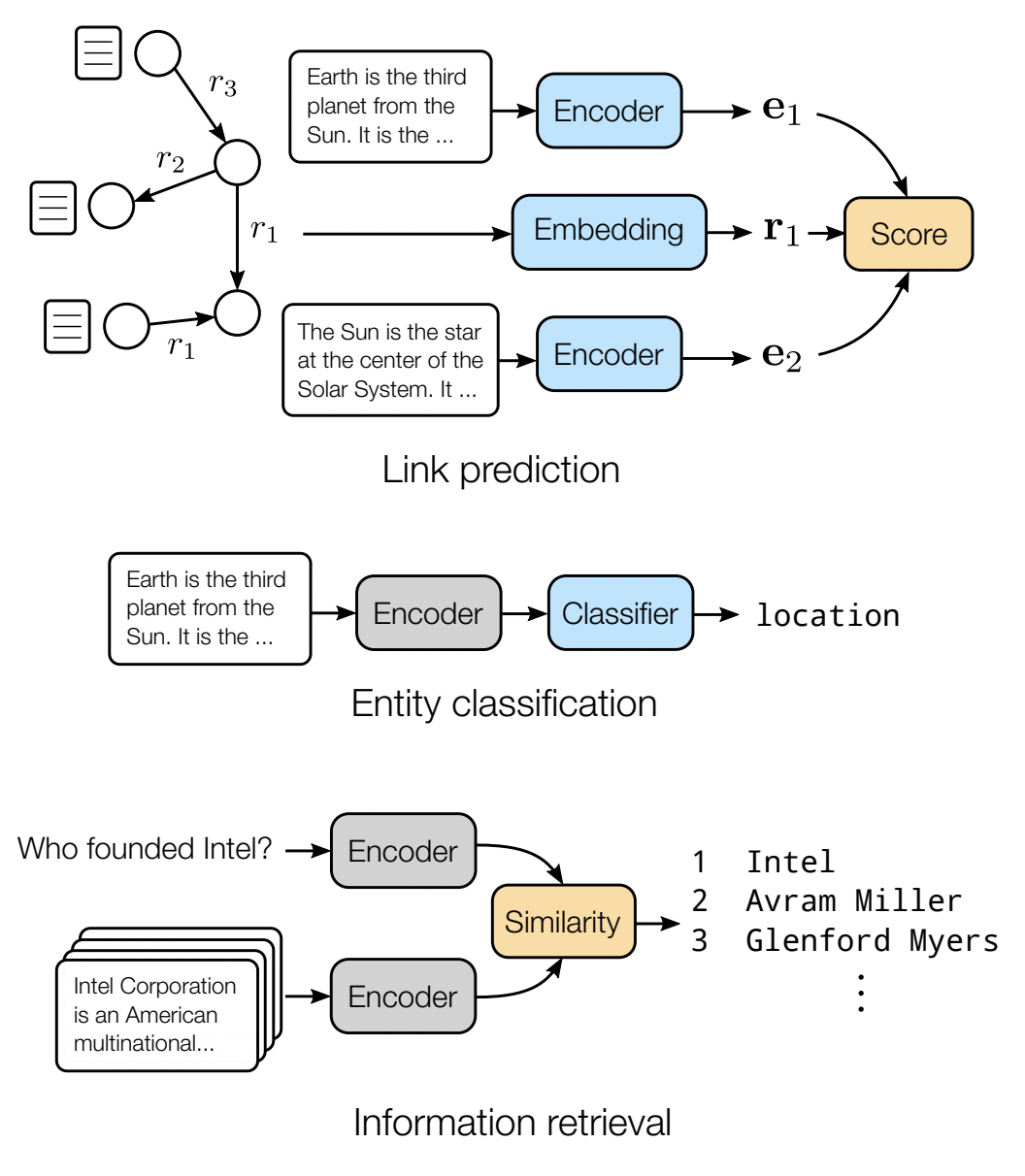Источник [21]

В графах, основанных на текстовых источниках (например как Wikidata и DBpedia завязаны на Wikipedia), часто можно найти текстовые описания вершин. Например rdfs:label и schema:description сущностей Wikidata содержат текст на естественном языке. Авторы [21] предложили метод BERT for Link Prediction (BLP) - использовать языковую модель (например, BERT [23]) как универсальный энкодер текстовых описаний в вектор признаков вершины. Построенные признаки затем можно связать с любым link prediction декодером (TransE, ComplEx и другими параметрическими или непараметрическими).

Преимуществом BLP является отсутствие обучаемых эмбеддингов вершин, что, при наличии текстовых описаний для всех сущностей, будь то известные или неизвестные, и пре-тренированного энкодера, позволяет использовать этот метод и в индуктивных сценариях. Эмбеддинги предикатов BLP обучаемые, но при наличии текстовых описаний предикатов их признаки можно получать так же через языковую модель.

Так как языковая модель - универсальный энкодер, то полученные представления могут использоваться не только для предсказания связей, но и для задач классификации (entity classification) и извлечения релевантных сущностей (information retrieval) при подключении подходящего декодера.

Structural Features

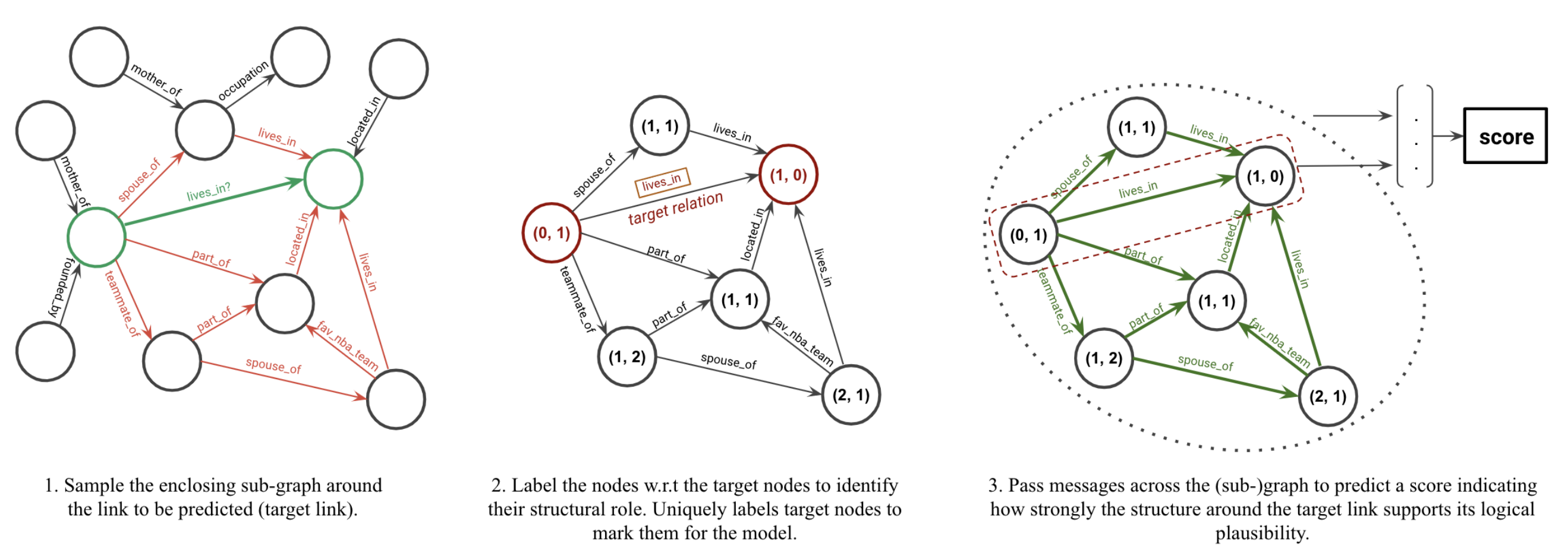Источник [22]

Самый сложный сценарий - на инференс приходит полностью новый граф без ребер к тренировочному графу и без доступных текстовых описаний вершин (однако, условие всех известных типов ребер на тренировке сохраняется). В этом случае, авторы алгоритма GraIL [22] предлагают использовать структурные графовые признаки вершин и сообществ для обучения графового энкодера (GNN), веса которого будут работать и на новых, неизвестных графах.

Построение признаков вершин

GraIL основан на идее агрегирования подграфов. Для каждого тренировочного триплета $(h,r,t)$, GraIL:

  1. Строит 1/2-hop подграф вокруг head и tail вершин
  2. Применяет процедуру назначения структурных признаков: для каждой вершины в подграфе ищется два числа $(d_h, d_t)$, где $d_h$ - кратчайший путь до head вершины триплета, $d_t$ - кратчайший путь до tail триплета. Сами head / tail вершины имеют, соответственно, признаки (0, 1) и (1,0). Кратчайшие пути можно искать, например, по алгоритму Дейкстры.
  3. Зная максимальную глубину всех подграфов, числовые признаки переводятся в one-hot encoded признаки. Например, при максимальной дистанции в 3 hops получается 8-размерный вектор признаков: 
    (0, 1): [1, 0, 0, 0, 0, 1, 0, 0]
(1, 0): [0, 1, 0, 0, 1, 0, 0, 0]

Получение вектора подграфа На этом шаге у каждой вершины подграфа есть вектор признаков. Затем GraIL

  1. Применяет модификацию R-GCN с признаками ребер (edge features) и механизмом внимания (attention) к подграфу;
  2. Сохранются обновленные представления $\mathbf{h}_u, \mathbf{h}_v, \mathbf{e}_{r} $ head / tail / типа ребра
  3. Обновленные представления всех вершин подграфа агрегируются, например, усредняются (average pooling), в один вектор $\mathbf{h}_G$;
  4. Финальный вектор строится из конкатенации $[ \mathbf{h}_G \bigoplus \mathbf{h}_u \bigoplus \mathbf{h}_v \bigoplus \mathbf{e}_{r} ]$ и используется для тренировки.

В силу вычислительной сложности семплирования подграфов и поиска кратчайших путей в каждом из них, GraIL тестировался на задаче предсказания предиката (relation prediction) вместо предсказания вершины в ребре (link prediction).

Преимущества:

  • Работает на полностью неизвестных графах с неизвестными вершинами
  • Не требует наличия каких-либо признаков или текстовых описаний
  • Единственные тренируемые параметры - эмбеддинги предикатов и веса R-GCN

Недостатки:

  • Высокая вычислительная сложность подготовки подграфов и инференса

Библиотеки и репозитории

Популярные библиотеки для работы с GNNs:

  • PyG - PyTorch Geometric (PyTorch)
  • DGL (PyTorch, MXNet, TensorFlow)
  • Jraph (Jax)

Домашнее задание

Познакомьтесь с основным инструментарием Graph ML в 4 colab notebooks:

  1. NetworkX + PyTorch Geometric
  2. Базовые статистики и эмбеддинги
  3. Тензоры PyTorch Geometric, Open Graph Benchmark, GCN
  4. GraphSAGE, GAT, DeepSnap

Использованные материалы и ссылки:

[0] Michael M. Bronstein, Joan Bruna, Taco Cohen, Petar Veličković. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges. 2021
[1] William L. Hamilton. Graph Representation Learning. Morgan and Claypool. 2020
[2] Sanchez-Lengeling, et al., “A Gentle Introduction to Graph Neural Networks”, Distill, 2021.
[3] Bryan Perozzi, Rami Al-Rfou, Steven Skiena. DeepWalk: Online Learning of Social Representations. KDD 2014.
[4] Aditya Grover and Jure Leskovec. node2vec: Scalable Feature Learning for Networks. KDD 2016
[5] Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, Qiaozhu Mei. LINE: Large-scale Information Network Embedding. WWW 2015
[6] Anton Tsitsulin, Davide Mottin, Panagiotis Karras, Emmanuel Müller. VERSE: Versatile Graph Embeddings from Similarity Measures. WWW 2018
[7] Keyulu Xu, Weihua Hu, Jure Leskovec, Stefanie Jegelka. How Powerful are Graph Neural Networks? ICLR 2019
[8] Gabriele Corso, Luca Cavalleri, Dominique Beaini, Pietro Liò, Petar Veličković. Principal Neighbourhood Aggregation for Graph Nets. NeurIPS 2020
[9] Yujia Li, Daniel Tarlow, Marc Brockschmidt, Richard Zemel. Gated Graph Sequence Neural Networks. ICLR 2016
[10] Thomas N. Kipf, Max Welling. Semi-Supervised Classification with Graph Convolutional Networks. ICLR 2017
[11] Lingxiao Zhao, Leman Akoglu. PairNorm: Tackling Oversmoothing in GNNs. ICLR 2020
[12] Uri Alon, Eran Yahav. On the Bottleneck of Graph Neural Networks and its Practical Implications. ICLR 2021
[13] Guohao Li, Matthias Müller, Bernard Ghanem, Vladlen Koltun. Training Graph Neural Networks with 1000 Layers. ICML 2021
[14] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio. Graph Attention Networks. ICLR 2018
[15] Battaglia et al. Relational inductive biases, deep learning, and graph networks. 2018
[16] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin. Attention Is All You Need. NIPS 2017.
[17] Michael Schlichtkrull, Thomas N. Kipf, Peter Bloem, Rianne van den Berg, Ivan Titov, Max Welling. Modeling Relational Data with Graph Convolutional Networks. ESWC 2018.
[18] Thiviyan Thanapalasingam, Lucas van Berkel, Peter Bloem, Paul Groth. Relational Graph Convolutional Networks: A Closer Look. arxiv 2021.
[19] Shikhar Vashishth, Soumya Sanyal, Vikram Nitin, Partha Talukdar. Composition-based Multi-Relational Graph Convolutional Networks. ICLR 2020.
[20] Marjan Albooyeh, Rishab Goel, Seyed Mehran Kazemi. Out-of-Sample Representation Learning for Multi-Relational Graphs. EMNLP 2020.
[21] Daniel Daza, Michael Cochez, Paul Groth. Inductive Entity Representations from Text via Link Prediction. WWW 2021.
[22] Komal K. Teru, Etienne Denis, William L. Hamilton. Inductive Relation Prediction by Subgraph Reasoning. ICML 2020.
[23] Jacob Devlin, Ming-Wei Chang, Kenton Lee, Kristina Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. NAACL 2019.